7 Out Of 20 Percentage
metako
Sep 21, 2025 · 5 min read
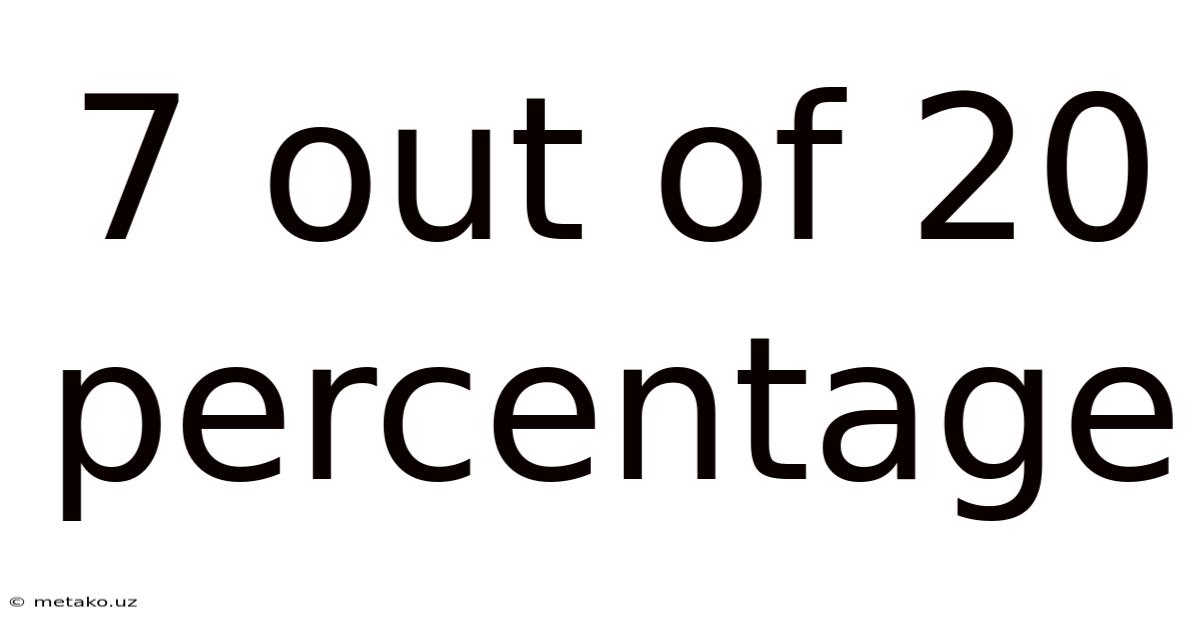
Table of Contents
Decoding 7 out of 20: Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts in a shop to analyzing financial reports. This article delves deep into the seemingly simple concept of "7 out of 20," explaining its calculation, practical applications, and the broader implications of percentage understanding. We'll explore different methods of calculation, address common misconceptions, and provide real-world examples to solidify your grasp of this crucial mathematical concept.
Introduction: What Does 7 out of 20 Mean?
"7 out of 20" represents a fraction where 7 is the part and 20 is the whole. It signifies that out of a total of 20 items, events, or quantities, 7 possess a specific characteristic or belong to a particular group. To express this as a percentage, we need to convert the fraction into a percentage value. This seemingly simple calculation underlies many complex statistical analyses and daily life decision-making processes. Understanding how to accurately and efficiently convert fractions to percentages is key to navigating various situations that demand percentage-based interpretations.
Calculating 7 out of 20 as a Percentage: Step-by-Step Guide
There are several ways to calculate the percentage equivalent of 7 out of 20. Let's explore the most common methods:
Method 1: Using the Fraction to Decimal Conversion
-
Express as a fraction: Write "7 out of 20" as a fraction: 7/20.
-
Convert to decimal: Divide the numerator (7) by the denominator (20): 7 ÷ 20 = 0.35.
-
Convert to percentage: Multiply the decimal by 100: 0.35 x 100 = 35%.
Therefore, 7 out of 20 is equal to 35%.
Method 2: Using Proportions
This method involves setting up a proportion to solve for the unknown percentage.
-
Set up the proportion: Let 'x' represent the percentage. We can set up the proportion: 7/20 = x/100
-
Cross-multiply: Multiply 7 by 100 and 20 by x: 700 = 20x
-
Solve for x: Divide both sides by 20: x = 700 ÷ 20 = 35
Therefore, x = 35%, confirming that 7 out of 20 is 35%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply enter 7 ÷ 20 and then multiply the result by 100 to obtain the percentage. This method is quick and efficient, especially for more complex calculations.
Understanding Percentage Applications: Real-World Examples
The concept of 7 out of 20, or 35%, finds application in many real-world scenarios:
-
Academic Performance: If a student answers 7 out of 20 questions correctly on a test, their score is 35%. This provides a clear measure of their understanding of the subject matter.
-
Sales and Discounts: A store offering a 35% discount on an item essentially reduces the price by 7 out of every 20 units of the original price.
-
Survey Results: If 7 out of 20 respondents in a survey agree with a particular statement, 35% of the respondents hold that opinion. This data is crucial in understanding public perception or market trends.
-
Sports Statistics: A basketball player who makes 7 out of 20 shots has a field goal percentage of 35%. This statistic reflects the player's shooting accuracy.
-
Quality Control: In manufacturing, if 7 out of 20 products fail a quality check, the defect rate is 35%. This information helps identify areas for improvement in the production process.
-
Financial Analysis: Analyzing financial statements often involves working with percentages. For example, if a company's profit margin is 35%, it means that 7 out of every 20 dollars of revenue is profit.
Common Misconceptions about Percentages
While percentages seem straightforward, some common misconceptions can lead to errors:
-
Confusing percentages with absolute values: A 35% increase in sales from 100 units to 135 units is different from a 35% increase from 1000 units to 1350 units, even though both represent a 35% increase. The absolute change in units is significantly larger in the second case.
-
Incorrectly calculating percentage changes: Calculating percentage increases or decreases requires careful attention to the base value. For instance, a decrease from 20 to 13 is not a 7% decrease; it's a 35% decrease (7/20 * 100%).
-
Misinterpreting percentages in context: A percentage value only makes sense within its specific context. A 35% approval rating for a political candidate is different from a 35% success rate for a medical treatment. Understanding the context is critical for accurate interpretation.
Advanced Applications and Extensions of Percentage Calculations
Beyond the basic calculation of 7 out of 20, understanding percentages opens doors to more advanced concepts:
-
Compound interest: Calculating compound interest involves repeatedly applying a percentage change to a base amount over time.
-
Statistical analysis: Many statistical measures, such as mean, median, mode, and standard deviation, are expressed as percentages or involve percentage calculations.
-
Financial modeling: Percentage calculations are essential in creating and interpreting financial models, forecasting future outcomes, and evaluating investment opportunities.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage increase or decrease?
To calculate a percentage increase, find the difference between the new value and the original value, divide the difference by the original value, and multiply by 100. For a percentage decrease, follow the same process.
Q2: How can I convert a percentage back to a fraction or decimal?
To convert a percentage to a decimal, divide the percentage by 100. To convert a percentage to a fraction, write the percentage as a fraction over 100 and simplify.
Q3: What are some common uses of percentages in everyday life?
Percentages are used in everyday life for calculating discounts, taxes, tips, interest rates, grades, and many other situations.
Q4: Are there any online tools or calculators that can help me with percentage calculations?
Yes, numerous online tools and calculators are available to assist with percentage calculations. Many calculators have built-in percentage functions.
Conclusion: Mastering Percentages – A Valuable Skill
Understanding how to calculate and interpret percentages is a critical skill for anyone, regardless of their profession or background. Starting with simple examples like "7 out of 20," and understanding the methods to convert fractions to percentages, builds a strong foundation. As you move beyond this basic example, the ability to confidently handle percentages will significantly enhance your ability to analyze data, make informed decisions, and navigate various aspects of your life effectively. Remember to pay close attention to the context, avoid common misconceptions, and practice regularly to master this essential mathematical skill.
Latest Posts
Latest Posts
-
How To Solve Rc Circuits
Sep 21, 2025
-
Is Heat A State Function
Sep 21, 2025
-
6 Signs Of Chemical Change
Sep 21, 2025
-
Positive Selection Vs Negative Selection
Sep 21, 2025
-
Why Are Ionic Substances Brittle
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 20 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.