I Prt Solve For R
metako
Sep 18, 2025 · 6 min read
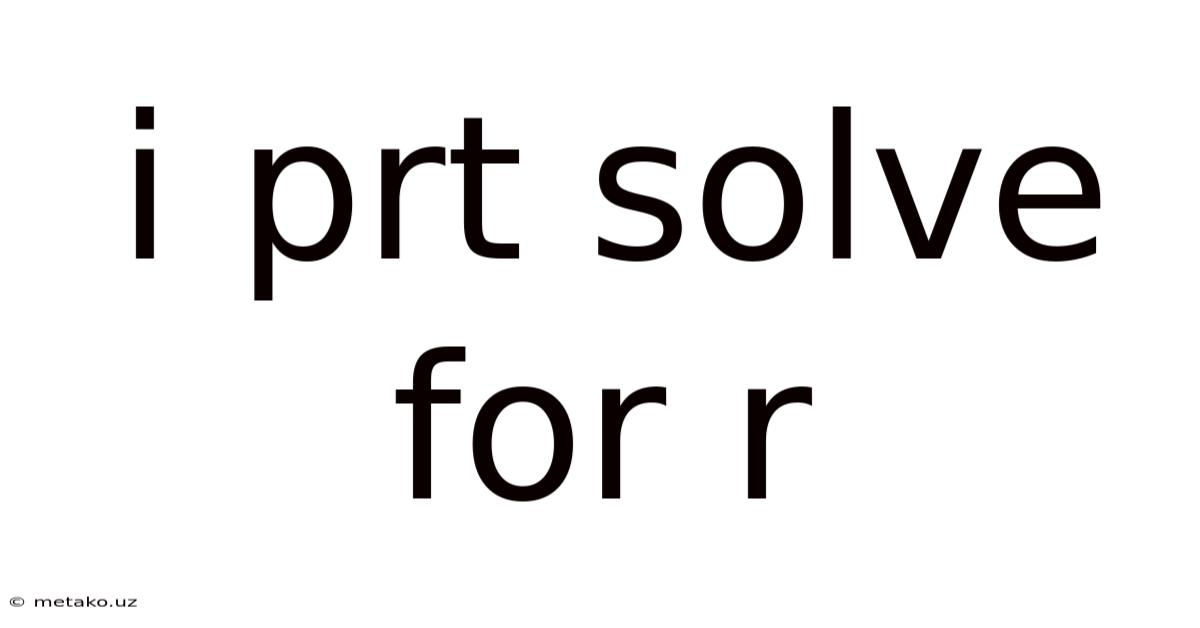
Table of Contents
Solving for 'r': A Comprehensive Guide to Isolating the Variable in Different Equations
This article provides a comprehensive guide to solving for the variable 'r' in various mathematical equations. We'll cover different scenarios, from simple linear equations to more complex formulas involving exponents and logarithms. Understanding how to isolate 'r' is a fundamental skill in algebra and is crucial for numerous applications in science, engineering, and finance. We'll break down the process step-by-step, ensuring a clear understanding for learners of all levels. Mastering this skill will significantly enhance your problem-solving capabilities in mathematics and related fields.
Understanding the Fundamentals: Isolating Variables
Before diving into specific examples, let's establish the core principle: solving for 'r' (or any variable) means manipulating the equation to get 'r' by itself on one side of the equals sign. This involves applying inverse operations to undo the mathematical operations performed on 'r'. Remember that whatever you do to one side of the equation, you must do to the other to maintain balance.
The common operations and their inverses are:
- Addition: The inverse is subtraction. If 'r + 5 = 10', subtract 5 from both sides.
- Subtraction: The inverse is addition. If 'r - 3 = 7', add 3 to both sides.
- Multiplication: The inverse is division. If '5r = 20', divide both sides by 5.
- Division: The inverse is multiplication. If 'r/2 = 6', multiply both sides by 2.
- Exponents: The inverse is taking the root (e.g., the square root for an exponent of 2). If 'r² = 9', take the square root of both sides.
- Logarithms: The inverse is exponentiation. If 'log₁₀(r) = 2', then r = 10².
Solving for 'r' in Simple Linear Equations
Let's start with straightforward examples involving linear equations. These equations have 'r' raised to the power of 1.
Example 1: Solve for 'r' in the equation 3r + 7 = 16.
- Isolate the term with 'r': Subtract 7 from both sides: 3r + 7 - 7 = 16 - 7 => 3r = 9
- Solve for 'r': Divide both sides by 3: 3r / 3 = 9 / 3 => r = 3
Example 2: Solve for 'r' in the equation (r/4) - 2 = 5
- Isolate the term with 'r': Add 2 to both sides: (r/4) - 2 + 2 = 5 + 2 => r/4 = 7
- Solve for 'r': Multiply both sides by 4: (r/4) * 4 = 7 * 4 => r = 28
Example 3: Solve for 'r' in the equation 2(r - 5) = 12
- Distribute: Expand the parentheses: 2r - 10 = 12
- Isolate the term with 'r': Add 10 to both sides: 2r - 10 + 10 = 12 + 10 => 2r = 22
- Solve for 'r': Divide both sides by 2: 2r / 2 = 22 / 2 => r = 11
Solving for 'r' in Equations with Exponents
When 'r' is raised to a power, we need to use roots to isolate it.
Example 4: Solve for 'r' in the equation r² = 25
- Take the square root: √r² = ±√25 => r = ±5 (Remember to consider both positive and negative roots)
Example 5: Solve for 'r' in the equation r³ + 8 = 35
- Isolate the term with 'r': Subtract 8 from both sides: r³ + 8 - 8 = 35 - 8 => r³ = 27
- Take the cube root: ³√r³ = ³√27 => r = 3
Example 6: Solve for 'r' in the equation 2r² - 10 = 18
- Isolate the term with r²: Add 10 to both sides: 2r² = 28
- Divide by 2: r² = 14
- Take the square root: r = ±√14
Solving for 'r' in Equations with Logarithms
Logarithms are the inverse of exponents. The equation logₐ(b) = c means aᶜ = b.
Example 7: Solve for 'r' in the equation log₂(r) = 4
- Rewrite in exponential form: 2⁴ = r
- Solve for r: r = 16
Example 8: Solve for 'r' in the equation ln(r) = 2 (ln denotes the natural logarithm, base e)
- Rewrite in exponential form: e² = r
- Solve for r: r ≈ 7.39 (using a calculator to approximate the value of e²)
Solving for 'r' in More Complex Equations
Many real-world applications involve more intricate equations. The approach remains the same: systematically isolate 'r' using inverse operations. These examples might require multiple steps and a careful order of operations.
Example 9: Solve for 'r' in the equation 5r + 3 = 2r + 11
- Combine like terms: Subtract 2r from both sides: 3r + 3 = 11
- Isolate the term with 'r': Subtract 3 from both sides: 3r = 8
- Solve for 'r': Divide both sides by 3: r = 8/3
Example 10: Solve for 'r' in the equation (r+2)/(r-1) = 3
- Multiply both sides by (r-1): r + 2 = 3(r - 1)
- Distribute: r + 2 = 3r - 3
- Combine like terms: Subtract r from both sides: 2 = 2r - 3
- Add 3 to both sides: 5 = 2r
- Solve for r: r = 5/2
Solving for 'r' in Formulas and Equations from other Fields
The principles we’ve discussed apply to various formulas across different scientific and mathematical disciplines. Here are a couple of examples:
Example 11 (Simple Interest): The formula for simple interest is I = Prt, where I is the interest, P is the principal, r is the interest rate, and t is the time. Solve for r.
- Divide both sides by Pt: I / (Pt) = r
Example 12 (Compound Interest): The formula for compound interest is A = P(1 + r/n)^(nt), where A is the final amount, P is the principal, r is the interest rate, n is the number of times interest is compounded per year, and t is the time in years. Solving for 'r' in this equation is more complex and typically requires logarithmic functions. Let's simplify by assuming n=1 (compounded annually):
A = P(1 + r)^t
- Divide by P: A/P = (1 + r)^t
- Take the t-th root: (A/P)^(1/t) = 1 + r
- Subtract 1: (A/P)^(1/t) - 1 = r
Frequently Asked Questions (FAQ)
Q: What if I get a negative value for 'r'?
A: A negative value for 'r' is perfectly acceptable in many contexts. Its meaning will depend on the specific equation and its application. For example, in financial calculations, a negative interest rate might represent a debt.
Q: What if I make a mistake?
A: Don't worry! Mistakes are a natural part of the learning process. Carefully review your steps, double-check your calculations, and try the problem again. If you're still stuck, seek help from a teacher, tutor, or online resources.
Q: Are there any online tools to help solve for 'r'?
A: Yes, many online calculators and solvers can help you check your work or solve more complex equations. However, it's crucial to understand the underlying process so you can apply it in various situations.
Conclusion
Solving for 'r' involves applying inverse operations to isolate the variable. We've covered various scenarios, from simple linear equations to those with exponents and logarithms. Remember to always maintain the balance of the equation and apply the order of operations correctly. Practice is key to mastering this essential algebraic skill. With consistent effort, you'll develop the confidence and ability to tackle increasingly complex equations, opening doors to further mathematical exploration and applications in various fields. The methods described here provide a strong foundation for solving for any variable in a wide range of mathematical problems.
Latest Posts
Latest Posts
-
Unit Conversion Problems Chemistry Practice
Sep 18, 2025
-
How To Draw Hydrogen Bonds
Sep 18, 2025
-
Electron Arrangement Of Aluminum Ion
Sep 18, 2025
-
Ln K Vs 1 T Graph
Sep 18, 2025
-
Electron Dot Structure Of Hydrogen
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about I Prt Solve For R . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.