Is 1/2 Greater Than 6/8
metako
Sep 14, 2025 · 5 min read
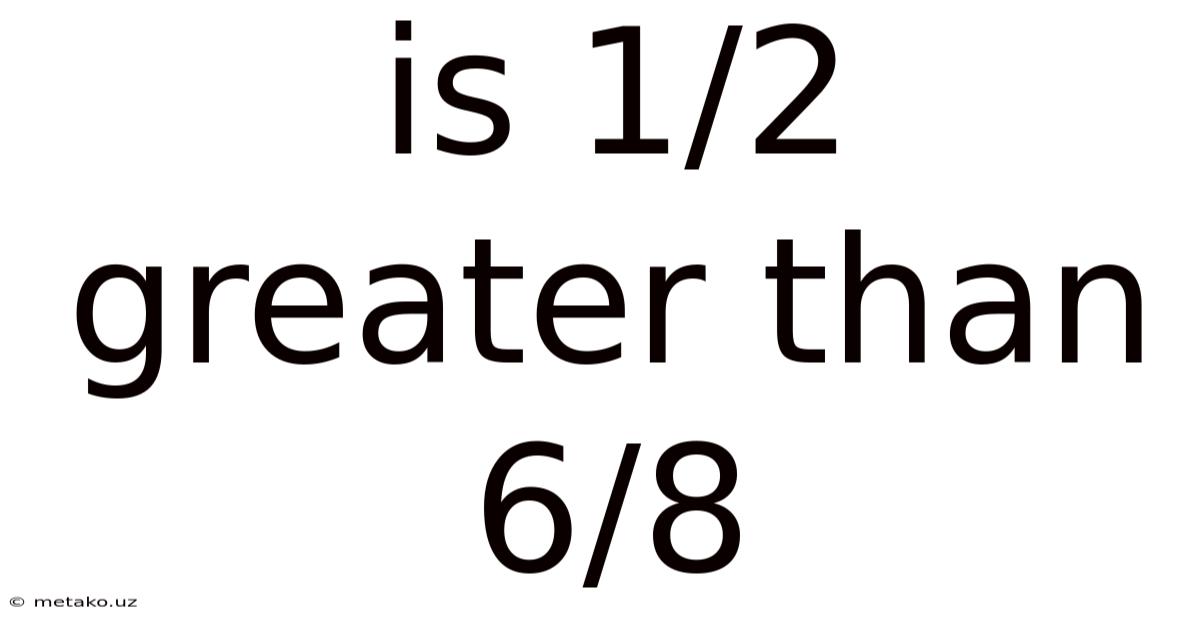
Table of Contents
Is 1/2 Greater Than 6/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, forming the bedrock for more advanced concepts. This article delves into the question: Is 1/2 greater than 6/8? We will not only answer this question definitively but also explore the various methods for comparing fractions, ensuring you gain a comprehensive understanding of this crucial mathematical principle. This will involve exploring equivalent fractions, simplifying fractions, and using visual representations to solidify your grasp of the concept.
Introduction to Fractions
Before we tackle the central question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is written in the form a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For instance, in the fraction 1/2, 1 is the numerator and 2 is the denominator, representing one out of two equal parts.
Understanding the relationship between the numerator and denominator is critical for comparing fractions. A larger numerator, keeping the denominator constant, indicates a larger fraction. Conversely, a larger denominator, keeping the numerator constant, indicates a smaller fraction.
Method 1: Simplifying Fractions
One of the most effective methods for comparing fractions is to simplify them to their simplest form. Simplifying a fraction means reducing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's simplify 6/8. The GCD of 6 and 8 is 2. Dividing both the numerator and denominator by 2, we get:
6 ÷ 2 / 8 ÷ 2 = 3/4
Now we can easily compare 1/2 and 3/4.
Method 2: Finding a Common Denominator
Another reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. The easiest way to do this is to find the least common multiple (LCM) of the two denominators. The LCM is the smallest number that is a multiple of both denominators.
In our case, the denominators are 2 and 4. The LCM of 2 and 4 is 4.
Let's convert 1/2 to a fraction with a denominator of 4:
To change the denominator from 2 to 4, we multiply it by 2. To maintain the value of the fraction, we must also multiply the numerator by 2:
(1 × 2) / (2 × 2) = 2/4
Now we can compare 2/4 and 3/4 directly.
Method 3: Visual Representation
Visual representations, such as pie charts or fraction bars, can be incredibly helpful, especially for beginners. Let's visualize 1/2 and 6/8 (or its simplified form, 3/4).
Imagine a circle divided into two equal parts. Shading one part represents 1/2.
Now imagine another circle, but this time divided into four equal parts. Shading three parts represents 3/4. By visually comparing the shaded areas, it's clear that 3/4 (or 6/8) represents a larger portion than 1/2.
Comparing 1/2 and 3/4 (or 6/8): The Conclusion
Using any of the methods above – simplifying fractions, finding a common denominator, or visual representation – we arrive at the same conclusion: No, 1/2 is not greater than 6/8. In fact, 6/8 (which simplifies to 3/4) is greater than 1/2.
3/4 represents a larger portion of the whole than 1/2. This is because 3/4 is equivalent to 6/8, and both are larger than 1/2.
Understanding Equivalent Fractions
The concept of equivalent fractions is crucial for understanding fraction comparison. Equivalent fractions represent the same portion of a whole, even though they have different numerators and denominators. For example, 1/2, 2/4, 3/6, 4/8, and so on, are all equivalent fractions. They all represent the same amount – one-half.
Understanding this concept allows us to simplify fractions and find common denominators, making comparisons much easier.
Decimal Representation for Comparison
While not always necessary, converting fractions to decimals can also aid in comparison.
1/2 = 0.5
6/8 = 3/4 = 0.75
A simple comparison of 0.5 and 0.75 clearly shows that 0.75 (or 3/4 or 6/8) is greater than 0.5 (or 1/2).
Advanced Fraction Comparison Techniques
For more complex fraction comparisons, particularly those involving multiple fractions, more advanced techniques may be necessary. These include:
-
Cross-multiplication: This method involves multiplying the numerator of one fraction by the denominator of the other and comparing the results. If a/b and c/d are the fractions, compare ad and bc. If ad > bc, then a/b > c/d.
-
Using a number line: Plotting fractions on a number line can provide a visual comparison, especially when dealing with a range of fractions.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand and compare. Working with simpler numbers reduces the complexity of calculations and improves clarity.
Q2: What if the denominators have no common factors?
A2: If the denominators have no common factors, you will need to find the least common multiple (LCM) to find a common denominator.
Q3: Can I always convert fractions to decimals for comparison?
A3: While converting to decimals can be helpful, it's not always practical, especially with fractions that result in repeating or non-terminating decimals. Working directly with fractions often provides a clearer and more exact comparison.
Q4: Are there any online tools to help compare fractions?
A4: Yes, many online calculators and websites can compare fractions and provide step-by-step solutions. However, understanding the underlying principles is crucial for mastering the concept.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics. By understanding the different methods – simplifying fractions, finding common denominators, visual representation, and using decimals – you can confidently compare any two fractions. This article provided a comprehensive guide, addressing the specific question of whether 1/2 is greater than 6/8, and extending the knowledge to encompass a broader understanding of fraction comparison techniques. Remember that practice is key to mastering this skill. The more you work with fractions, the more intuitive and effortless the comparison process will become. Consistent practice and a thorough understanding of the underlying principles will empower you to confidently tackle more advanced mathematical concepts that build upon this foundation.
Latest Posts
Latest Posts
-
How To Calculate Solution Percentage
Sep 15, 2025
-
Mass Spectrum Of An Element
Sep 15, 2025
-
What Is A Speaking Outline
Sep 15, 2025
-
What Is An Ionic Solid
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 6/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.