Is 2/5 Greater Than 1/2
metako
Sep 22, 2025 · 5 min read
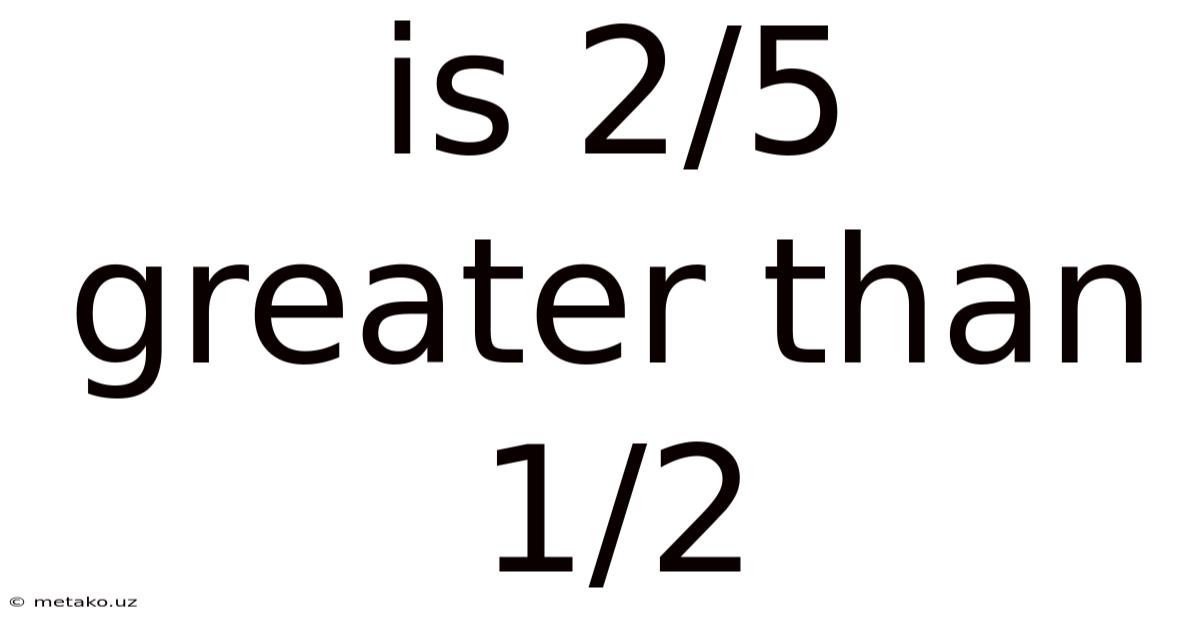
Table of Contents
Is 2/5 Greater Than 1/2? A Deep Dive into Fraction Comparison
This article explores the seemingly simple question: Is 2/5 greater than 1/2? While the answer might seem immediately obvious to some, a deeper understanding of fraction comparison provides valuable insights into fundamental mathematical concepts. We'll delve into various methods for comparing fractions, explain the underlying principles, and address common misconceptions. This comprehensive guide will equip you with the skills to confidently compare any two fractions.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) and a denominator (the bottom number), separated by a line (a fraction bar). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 2/5, the numerator is 2 and the denominator is 5. This means we have 2 out of 5 equal parts of a whole.
Method 1: Visual Comparison (Using Diagrams)
One of the most intuitive ways to compare fractions is through visual representation. Let's create diagrams to represent 2/5 and 1/2.
Imagine a rectangle divided into five equal parts. Shade two of these parts to represent 2/5. Now, imagine another rectangle of the same size, divided into two equal parts. Shade one of these parts to represent 1/2. By visually comparing the shaded areas, it becomes clear that the shaded area representing 1/2 is larger than the shaded area representing 2/5. Therefore, 1/2 > 2/5.
Method 2: Finding a Common Denominator
This is a more formal and widely applicable method. To compare fractions, we need to express them with a common denominator – a denominator that is a multiple of both denominators. The common denominator is essentially the "lowest common multiple" (LCM) of the two denominators.
-
Finding the LCM of 5 and 2: The multiples of 5 are 5, 10, 15, 20... The multiples of 2 are 2, 4, 6, 8, 10... The smallest number common to both lists is 10. Therefore, the LCM of 5 and 2 is 10.
-
Converting the fractions:
- To convert 2/5 to a fraction with a denominator of 10, we multiply both the numerator and the denominator by 2: (2 x 2) / (5 x 2) = 4/10
- To convert 1/2 to a fraction with a denominator of 10, we multiply both the numerator and the denominator by 5: (1 x 5) / (2 x 5) = 5/10
-
Comparing the equivalent fractions: Now we compare 4/10 and 5/10. Since 5/10 > 4/10, we conclude that 1/2 > 2/5.
Method 3: Converting to Decimals
Another effective method involves converting fractions to decimals. This method relies on the understanding that fractions represent division.
-
Converting 2/5 to a decimal: 2 ÷ 5 = 0.4
-
Converting 1/2 to a decimal: 1 ÷ 2 = 0.5
-
Comparing the decimals: Now we compare 0.4 and 0.5. Since 0.5 > 0.4, we conclude that 1/2 > 2/5.
Method 4: Cross-Multiplication
This is a quick method for comparing fractions, especially when finding a common denominator seems cumbersome. Cross-multiplication involves multiplying the numerator of one fraction by the denominator of the other, and vice-versa.
-
Cross-multiplying:
- Multiply the numerator of 2/5 (which is 2) by the denominator of 1/2 (which is 2): 2 x 2 = 4
- Multiply the numerator of 1/2 (which is 1) by the denominator of 2/5 (which is 5): 1 x 5 = 5
-
Comparing the products: Compare the two products: 4 and 5. Since 5 > 4, the fraction with the larger product (1/2) is the greater fraction. Therefore, 1/2 > 2/5.
Why Understanding Fraction Comparison Matters
The ability to compare fractions is crucial for numerous applications across various fields, including:
- Everyday life: Comparing prices, measuring ingredients, understanding proportions.
- Science and engineering: Analyzing data, calculating ratios, designing structures.
- Finance: Calculating interest rates, managing budgets, understanding financial statements.
- Cooking and baking: Following recipes, scaling ingredients.
Addressing Common Misconceptions
- Larger numerator always means a larger fraction: This is false unless the denominators are the same. For example, 2/5 is smaller than 1/2, even though 2 is greater than 1.
- Ignoring the denominator: The denominator is just as important as the numerator. It defines the size of the parts.
- Difficulty with large numbers: While dealing with large numbers might seem daunting, the principles of comparison remain the same. The methods discussed above (common denominator, decimals, cross-multiplication) work equally well with larger numbers.
Frequently Asked Questions (FAQ)
Q: Can I always use cross-multiplication to compare fractions?
A: Yes, cross-multiplication is a reliable method for comparing two fractions. It's particularly efficient when dealing with fractions that don't have easily identifiable common denominators.
Q: Which method is the best for comparing fractions?
A: The "best" method depends on the specific fractions and your personal preference. Visual comparison is excellent for building intuition, while the common denominator method provides a clear and systematic approach. Decimal conversion is useful when working with calculators, and cross-multiplication offers a quick way to compare fractions without calculating the LCM.
Q: What if the fractions are negative?
A: When comparing negative fractions, the principles remain the same, but remember that a larger negative number is actually smaller in value. For example, -2/5 is greater than -1/2 because -0.4 > -0.5.
Q: How can I practice comparing fractions?
A: The best way to practice is to work through various examples. Start with simpler fractions and gradually increase the difficulty. Online resources and textbooks offer plenty of practice problems. You can also create your own word problems involving fractions to reinforce your understanding.
Conclusion
The answer to the question "Is 2/5 greater than 1/2?" is definitively no. We've explored four different methods to demonstrate this: visual comparison, finding a common denominator, converting to decimals, and cross-multiplication. Each method offers a unique approach to comparing fractions, highlighting the importance of understanding the underlying concepts of numerators, denominators, and equivalent fractions. Mastering these techniques will enhance your mathematical skills and empower you to tackle more complex fraction-related problems with confidence. Remember to choose the method that best suits your understanding and the specific fractions you're comparing. With practice, comparing fractions will become second nature!
Latest Posts
Latest Posts
-
Is Expiration Active Or Passive
Sep 22, 2025
-
What Are Free Nerve Endings
Sep 22, 2025
-
General Purpose Of A Speech
Sep 22, 2025
-
Activation Energy Of Electronic Conductivity
Sep 22, 2025
-
Does Aluminum Need Roman Numerals
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 2/5 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.