Is 3/4 Or 3/8 Bigger
metako
Sep 09, 2025 · 6 min read
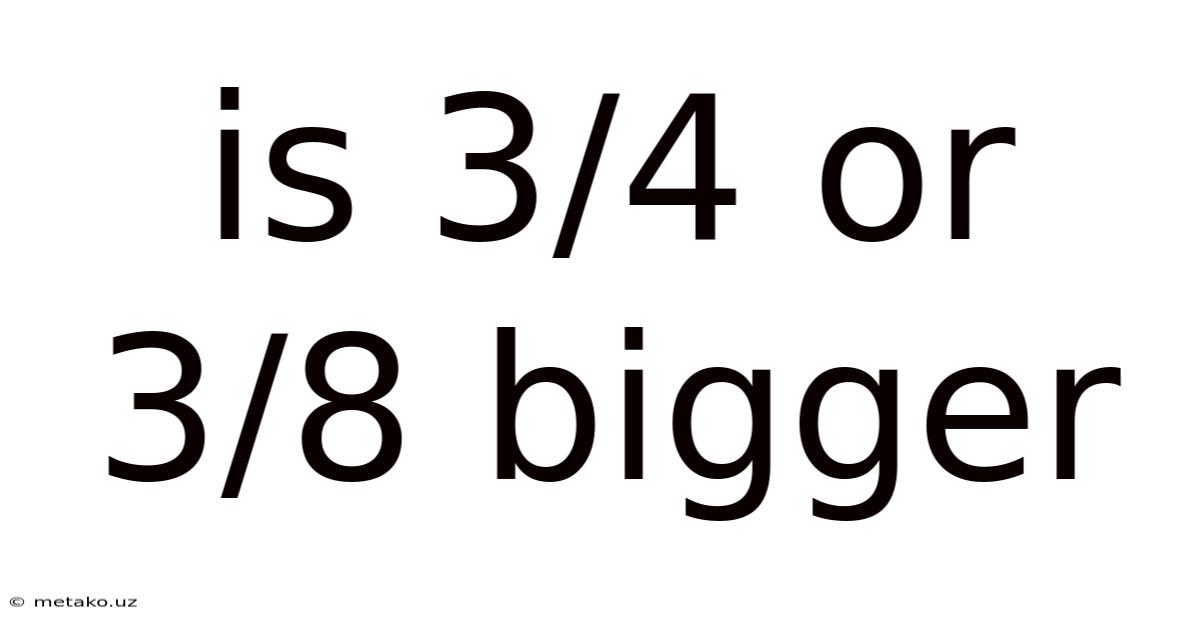
Table of Contents
Is 3/4 or 3/8 Bigger? Understanding Fractions and Their Comparison
Understanding fractions is a fundamental concept in mathematics, essential for everyday life and advanced studies. This article will thoroughly explore the question: "Is 3/4 or 3/8 bigger?" We'll delve into the core principles of comparing fractions, offering various methods to determine which fraction is larger, and provide practical examples to solidify your understanding. This comprehensive guide will not only answer the initial question but also equip you with the tools to compare any two fractions effectively.
Introduction to Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the denominator 4 means the whole is divided into four equal parts, and the numerator 3 indicates we are considering three of those parts.
Comparing Fractions: The Core Concepts
Comparing fractions involves determining which fraction represents a larger portion of the whole. There are several methods to achieve this:
1. Visual Representation:
This method is particularly helpful for beginners. Imagine two identical circles. Divide the first circle into four equal parts and shade three of them (representing 3/4). Divide the second circle into eight equal parts and shade three of them (representing 3/8). Visually, it's clear that the three-quarters circle has a larger shaded area than the three-eighths circle. This visual comparison makes it evident that 3/4 is greater than 3/8.
2. Common Denominator Method:
This is a robust and widely used method. To compare fractions, we need to find a common denominator—a number that is a multiple of both denominators. For 3/4 and 3/8, the least common multiple (LCM) of 4 and 8 is 8.
- We convert 3/4 to an equivalent fraction with a denominator of 8. To do this, we multiply both the numerator and denominator of 3/4 by 2: (3 x 2) / (4 x 2) = 6/8.
- Now we can easily compare 6/8 and 3/8. Since 6 > 3, we conclude that 6/8 (which is equivalent to 3/4) is greater than 3/8.
3. Decimal Conversion Method:
Converting fractions to decimals provides another way to compare them. We divide the numerator by the denominator for each fraction:
- 3/4 = 0.75
- 3/8 = 0.375
Since 0.75 > 0.375, we again conclude that 3/4 is greater than 3/8.
4. Comparing Numerators (when denominators are the same):
If two fractions have the same denominator, comparing them is straightforward. The fraction with the larger numerator is the larger fraction. For example, if we were comparing 5/8 and 3/8, we would immediately know that 5/8 is larger because 5 > 3. This method simplifies the comparison when a common denominator already exists.
5. Cross-Multiplication Method:
This method is particularly useful when finding a common denominator is cumbersome. We cross-multiply the numerators and denominators:
- Multiply the numerator of the first fraction by the denominator of the second fraction: 3 x 8 = 24
- Multiply the numerator of the second fraction by the denominator of the first fraction: 3 x 4 = 12
- Compare the results: 24 > 12. Since the product of the first fraction's numerator and the second fraction's denominator is greater, the first fraction (3/4) is larger.
Illustrative Examples: Applying the Methods
Let's apply the methods learned to compare other fractions.
Example 1: Comparing 2/3 and 5/6
- Common Denominator: The LCM of 3 and 6 is 6. We convert 2/3 to 4/6. Since 4/6 < 5/6, 5/6 is larger.
- Decimal Conversion: 2/3 ≈ 0.667, 5/6 ≈ 0.833. Again, 5/6 is larger.
- Cross-Multiplication: (2 x 6) = 12, (5 x 3) = 15. Since 12 < 15, 5/6 is larger.
Example 2: Comparing 7/10 and 3/5
- Common Denominator: The LCM of 10 and 5 is 10. We convert 3/5 to 6/10. Since 7/10 > 6/10, 7/10 is larger.
- Decimal Conversion: 7/10 = 0.7, 3/5 = 0.6. Again, 7/10 is larger.
- Cross-Multiplication: (7 x 5) = 35, (3 x 10) = 30. Since 35 > 30, 7/10 is larger.
A Deeper Dive: Understanding the Relationship Between Numerator and Denominator
The relative sizes of the numerator and denominator significantly impact the value of a fraction.
- Numerator < Denominator: The fraction is less than 1 (a proper fraction). For example, 3/4, 2/5, 7/10.
- Numerator = Denominator: The fraction equals 1 (a whole). For example, 4/4, 5/5, 10/10.
- Numerator > Denominator: The fraction is greater than 1 (an improper fraction). For example, 5/3, 8/5, 12/10. These can also be expressed as mixed numbers (a whole number and a proper fraction). For instance, 5/3 = 1 2/3.
Understanding this relationship helps in intuitively estimating the size of a fraction before applying formal comparison methods.
Frequently Asked Questions (FAQ)
Q1: What if the fractions have very large numbers?
A1: The methods described above still apply. While finding the LCM for extremely large numbers might be challenging, decimal conversion or cross-multiplication remain efficient alternatives. Using a calculator can significantly simplify the calculations.
Q2: Can I use a number line to compare fractions?
A2: Absolutely! A number line provides a visual representation of the relative positions of fractions. Plotting the fractions on a number line allows for a quick comparison of their magnitudes.
Q3: Are there any shortcuts for comparing fractions?
A3: If the denominators are close multiples of each other (like in 3/4 and 6/8), the visual representation or a quick mental conversion often suffices. For fractions with the same numerator, the fraction with the smaller denominator will always be larger.
Q4: Why is it important to learn how to compare fractions?
A4: Comparing fractions is a fundamental skill with numerous applications in various fields. It's crucial for understanding proportions, ratios, and percentages. It plays a critical role in problem-solving in areas like cooking, construction, finance, and even everyday tasks like sharing equally.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics. This article has explored multiple methods for comparing fractions, ranging from visual representations to more advanced techniques like cross-multiplication and decimal conversion. By mastering these methods and understanding the underlying principles of fractions, you'll be well-equipped to tackle any fraction comparison problem and apply this knowledge to real-world situations. Remember that the key is to choose the method that works best for you and the specific fractions being compared. Practice is vital; the more you practice comparing fractions, the more intuitive and efficient you will become. So grab a pencil and paper, try out some examples, and watch your understanding of fractions soar!
Latest Posts
Latest Posts
-
Strong Acids And Bases Chart
Sep 09, 2025
-
Graph Of A Non Function
Sep 09, 2025
-
Antibiotic Susceptibility Test Lab Report
Sep 09, 2025
-
Atomic Orbital Vs Molecular Orbital
Sep 09, 2025
-
Anatomy Of A Flowering Plant
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Or 3/8 Bigger . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.