Is 4/5 Greater Than 2/3
metako
Sep 19, 2025 · 6 min read
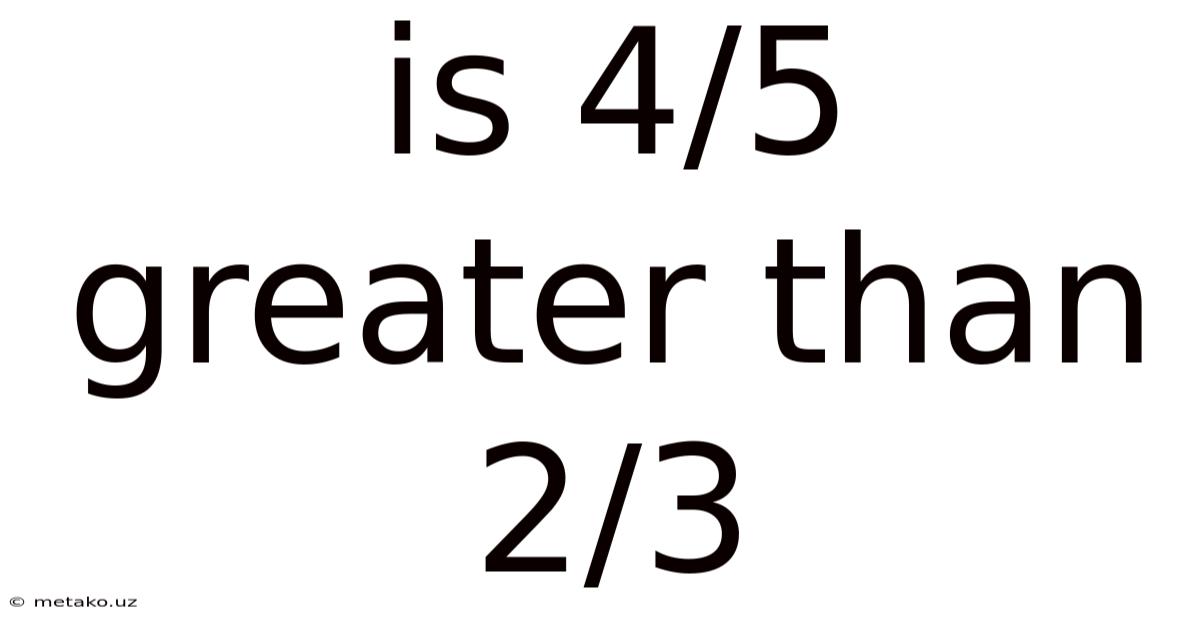
Table of Contents
Is 4/5 Greater Than 2/3? A Deep Dive into Fraction Comparison
Is 4/5 greater than 2/3? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. While the answer might seem obvious to some, understanding why 4/5 is greater than 2/3 requires exploring various methods of fraction comparison. This article will not only answer the question definitively but also equip you with the tools to compare any two fractions with confidence. We'll delve into the underlying principles, explore multiple comparison techniques, and address common misconceptions. This comprehensive guide will leave you with a firm grasp of fraction comparison, empowering you to tackle more complex mathematical problems.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the basics of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 4/5, the numerator is 4 and the denominator is 5. This means we have 4 out of 5 equal parts of a whole.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can simply compare the numerators. The fraction with the larger numerator is the larger fraction.
Let's apply this to our example: 4/5 and 2/3.
-
Find the least common multiple (LCM) of the denominators: The denominators are 5 and 3. The LCM of 5 and 3 is 15 (because 15 is the smallest number divisible by both 5 and 3).
-
Convert each fraction to an equivalent fraction with the common denominator:
-
To convert 4/5 to a fraction with a denominator of 15, we multiply both the numerator and denominator by 3: (4 x 3) / (5 x 3) = 12/15
-
To convert 2/3 to a fraction with a denominator of 15, we multiply both the numerator and denominator by 5: (2 x 5) / (3 x 5) = 10/15
-
-
Compare the numerators: Now we have 12/15 and 10/15. Since 12 > 10, we conclude that 12/15 > 10/15, and therefore, 4/5 > 2/3.
Method 2: Converting to Decimals
Another effective way to compare fractions is to convert them into decimals. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
To convert a fraction to a decimal, simply divide the numerator by the denominator.
-
Convert 4/5 to a decimal: 4 ÷ 5 = 0.8
-
Convert 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667 (this is a repeating decimal)
-
Compare the decimals: Since 0.8 > 0.6667, we can conclude that 4/5 > 2/3.
Method 3: Visual Representation
While not as precise as the previous methods for complex fractions, visualizing fractions using diagrams can provide an intuitive understanding. Imagine two identical circles.
-
Represent 4/5: Divide the first circle into 5 equal slices and shade 4 of them.
-
Represent 2/3: Divide the second circle into 3 equal slices and shade 2 of them.
By visually comparing the shaded areas, it becomes clear that the shaded portion of the circle representing 4/5 is larger than the shaded portion representing 2/3. This visual representation reinforces the conclusion that 4/5 > 2/3.
Method 4: Cross-Multiplication
Cross-multiplication is a shortcut method for comparing two fractions. It involves multiplying the numerator of one fraction by the denominator of the other and vice versa.
-
Cross-multiply: Multiply the numerator of 4/5 (which is 4) by the denominator of 2/3 (which is 3): 4 x 3 = 12
-
Cross-multiply: Multiply the numerator of 2/3 (which is 2) by the denominator of 4/5 (which is 5): 2 x 5 = 10
-
Compare the products: Since 12 > 10, we conclude that 4/5 > 2/3. The larger product corresponds to the larger fraction.
Understanding the Magnitude of the Difference
While we've established that 4/5 is greater than 2/3, it's also useful to understand the magnitude of this difference. By converting both fractions to decimals, we find that 4/5 is 0.8 and 2/3 is approximately 0.6667. The difference is approximately 0.1333, which represents a significant portion of the whole.
Addressing Common Misconceptions
A common misconception is that simply comparing numerators or denominators independently will determine which fraction is larger. This is incorrect. For instance, 2/3 might seem smaller than 4/5 because the numerator is smaller, but we need to consider the denominator as well. The denominator indicates the size of each part, influencing the overall magnitude of the fraction. This is why finding a common denominator or converting to decimals is crucial for accurate comparison.
Frequently Asked Questions (FAQ)
Q: Can I use any common denominator, or does it have to be the least common multiple (LCM)?
A: While using the LCM simplifies the calculations, you can use any common denominator. However, using the LCM keeps the numbers smaller and makes the comparison easier.
Q: Is there a fastest method for comparing fractions?
A: The fastest method often depends on the specific fractions involved. For simple fractions, cross-multiplication can be quick. For fractions that are difficult to convert to a common denominator, converting to decimals might be more efficient.
Q: What if the fractions are mixed numbers (a whole number and a fraction)?
A: Convert the mixed numbers into improper fractions (where the numerator is larger than the denominator) before applying any of the comparison methods discussed above.
Conclusion
Determining whether 4/5 is greater than 2/3 is not merely about arriving at a yes or no answer. It's an opportunity to solidify your understanding of fractions and master various comparison techniques. By applying the methods of finding a common denominator, converting to decimals, visual representation, or cross-multiplication, you can confidently compare any two fractions. Remember that understanding the underlying principles, rather than just memorizing a process, is key to building a strong foundation in mathematics. Mastering fraction comparison lays the groundwork for tackling more complex mathematical concepts in the future. The ability to confidently work with fractions is a crucial skill in various fields, from cooking and construction to advanced scientific calculations. This knowledge will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Color Coding The Periodic Table
Sep 19, 2025
-
Age Structure Definition Environmental Science
Sep 19, 2025
-
Stage Clips On A Microscope
Sep 19, 2025
-
Are K Selected Species Semelparous
Sep 19, 2025
-
How Do I Graph Y
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Is 4/5 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.