Lcm For 8 And 4
metako
Sep 22, 2025 · 6 min read
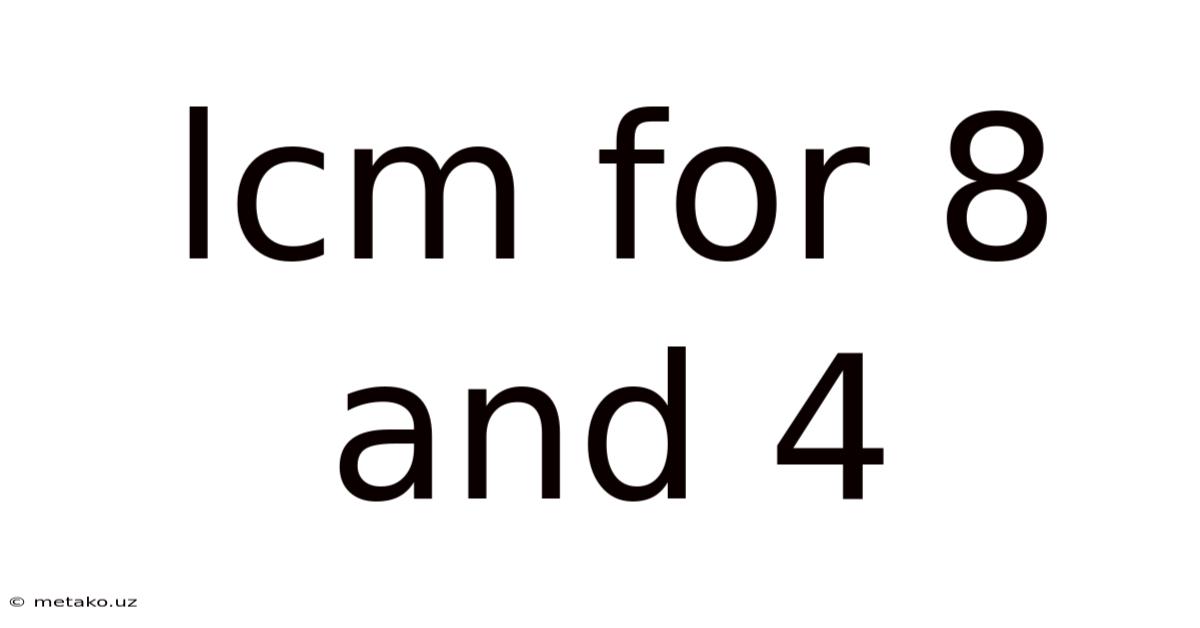
Table of Contents
Finding the Least Common Multiple (LCM) of 8 and 4: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This article provides a comprehensive guide to calculating the LCM of 8 and 4, exploring various methods and delving into the underlying mathematical principles. Understanding LCM is essential for anyone studying arithmetic, algebra, or number theory. We'll move beyond a simple calculation and explore the "why" behind the methods, making this concept clear and intuitive.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For instance, if we consider the numbers 2 and 3, their LCM is 6 because 6 is the smallest number divisible by both 2 and 3. This concept is widely used in various mathematical operations, particularly when dealing with fractions and simplifying expressions.
Let's focus on our specific example: finding the LCM of 8 and 4.
Method 1: Listing Multiples
One straightforward method to find the LCM is by listing the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
By comparing the two lists, we can see that the smallest number appearing in both lists is 8. Therefore, the LCM of 8 and 4 is 8.
This method is simple and intuitive, especially for smaller numbers. However, for larger numbers, it can become time-consuming and impractical.
Method 2: Prime Factorization
A more efficient and systematic method involves using prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 8 and 4:
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 4: 2 x 2 = 2²
Now, to find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
The only prime factor in both numbers is 2. The highest power of 2 is 2³ (from the factorization of 8). Therefore, the LCM of 8 and 4 is 2³ = 8.
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers. It provides a structured approach, making it less prone to errors.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. We can use the following formula to relate the LCM and GCD:
LCM(a, b) * GCD(a, b) = a * b
where 'a' and 'b' are the two integers.
First, let's find the GCD of 8 and 4. The divisors of 8 are 1, 2, 4, and 8. The divisors of 4 are 1, 2, and 4. The greatest common divisor is 4.
Now, we can use the formula:
LCM(8, 4) * GCD(8, 4) = 8 * 4 LCM(8, 4) * 4 = 32 LCM(8, 4) = 32 / 4 LCM(8, 4) = 8
This method demonstrates the elegant relationship between LCM and GCD. Knowing the GCD can significantly simplify the calculation of the LCM, especially for larger numbers where prime factorization might be more challenging.
Understanding the Relationship between LCM and GCD
The relationship between the LCM and GCD is fundamental in number theory. They provide complementary information about the divisibility properties of two numbers. The formula LCM(a, b) * GCD(a, b) = a * b highlights this interconnectedness. Understanding this relationship allows for efficient calculation of either LCM or GCD if one is already known. This is particularly useful in more advanced mathematical contexts.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
- Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
- Scheduling Problems: LCM is useful in solving problems related to scheduling events that occur at regular intervals (e.g., buses arriving at a stop, machines completing cycles). The LCM determines when these events will occur simultaneously.
- Modular Arithmetic: LCM plays a crucial role in modular arithmetic, which is used in cryptography and computer science.
- Music Theory: LCM is used to determine the least common multiple of musical note durations, helping in harmonizing and composing music.
Illustrative Examples
Let's consider a few more examples to solidify our understanding:
Example 1: Find the LCM of 12 and 18.
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
The highest power of 2 is 2², and the highest power of 3 is 3². Therefore, LCM(12, 18) = 2² x 3² = 4 x 9 = 36
Example 2: Find the LCM of 15 and 25.
- Prime factorization of 15: 3 x 5
- Prime factorization of 25: 5²
The highest power of 3 is 3, and the highest power of 5 is 5². Therefore, LCM(15, 25) = 3 x 5² = 3 x 25 = 75
Example 3: Find the LCM of 6, 9, and 12.
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3²
- Prime factorization of 12: 2² x 3
The highest power of 2 is 2², and the highest power of 3 is 3². Therefore, LCM(6, 9, 12) = 2² x 3² = 4 x 9 = 36
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder. They are inversely related, as shown by the formula LCM(a, b) * GCD(a, b) = a * b.
Q2: Can the LCM of two numbers be equal to one of the numbers?
A2: Yes, this happens when one number is a multiple of the other. As we saw in our example of 8 and 4, the LCM was 8, which is one of the original numbers.
Q3: How do I find the LCM of more than two numbers?
A3: You can extend the prime factorization method. Find the prime factorization of each number, then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to get the LCM.
Q4: Is there a limit to how large the LCM can be?
A4: No, there's no upper limit. As the numbers increase, the LCM can become arbitrarily large.
Q5: Are there any online calculators to find the LCM?
A5: While there are many online calculators available to compute the LCM, understanding the underlying methods is crucial for applying the concept in different mathematical situations and problem-solving.
Conclusion
Finding the least common multiple is a fundamental mathematical skill with broad applications. While the simple method of listing multiples works for smaller numbers, prime factorization offers a more efficient and systematic approach, especially for larger numbers. Understanding the relationship between LCM and GCD further enhances our ability to solve problems involving divisibility and multiples. Mastering the concept of LCM provides a solid foundation for tackling more advanced mathematical concepts and real-world applications. Remember to practice regularly to build proficiency and confidence in this essential area of mathematics.
Latest Posts
Latest Posts
-
Difference Between Cultural And Social
Sep 22, 2025
-
Logic Valid And Invalid Arguments
Sep 22, 2025
-
Do Acids Dissolve In Water
Sep 22, 2025
-
Definition Of A Rational Function
Sep 22, 2025
-
Teacher Centered Vs Student Centered
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 8 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.