Lcm Of 10 And 4
metako
Sep 14, 2025 · 6 min read
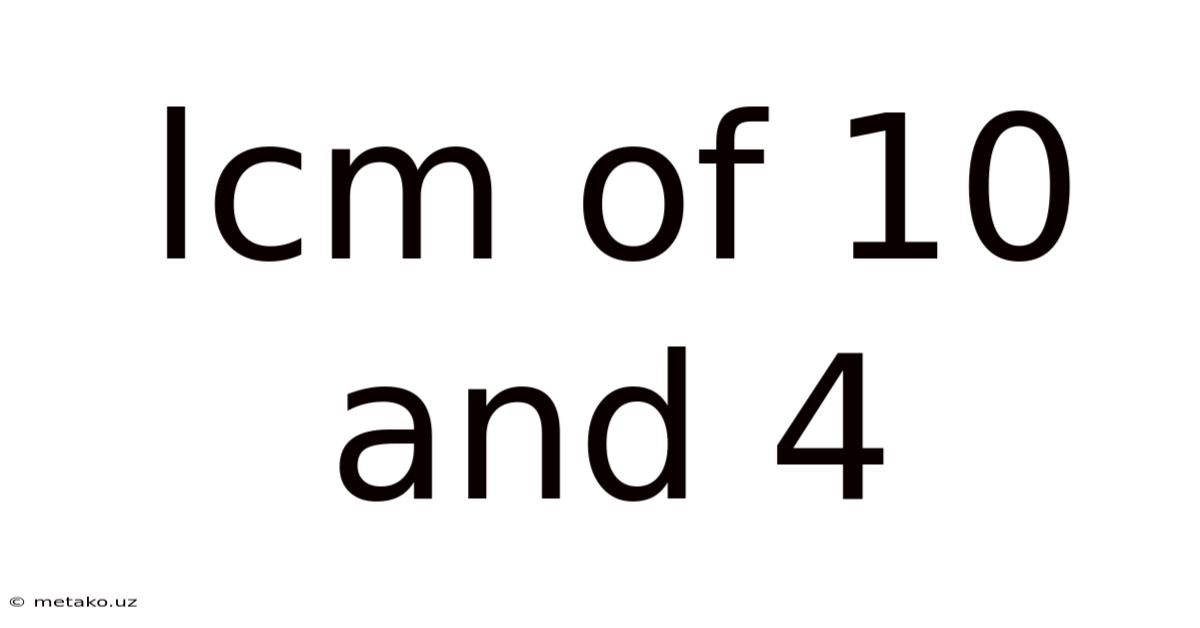
Table of Contents
Finding the LCM of 10 and 4: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex algebraic problems. This article will delve into the process of finding the LCM of 10 and 4, exploring different methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the broader significance of LCMs and their practical applications. This guide is perfect for students learning about LCMs, teachers looking for supplementary material, or anyone seeking a refresher on this important mathematical concept.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 10 and 4, let's establish a clear understanding of what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly, leaving no remainder.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method to find the LCM, especially for smaller numbers like 10 and 4, is by listing the multiples of each number until a common multiple is found.
- Multiples of 10: 10, 20, 30, 40, 50, 60...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
As you can see, the smallest number that appears in both lists is 20. Therefore, the LCM of 10 and 4 is 20. This method is straightforward and easy to visualize, making it ideal for beginners. However, for larger numbers, this method can become quite tedious and time-consuming.
Method 2: Prime Factorization
A more efficient and systematic method for finding the LCM, especially for larger numbers, is using prime factorization. This method involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's apply this to 10 and 4:
- Prime factorization of 10: 2 x 5
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together.
In this case, the prime factors are 2 and 5. The highest power of 2 is 2² (from the factorization of 4), and the highest power of 5 is 5¹ (from the factorization of 10).
Therefore, the LCM of 10 and 4 is 2² x 5 = 4 x 5 = 20.
This method is more efficient than listing multiples, particularly when dealing with larger numbers or a greater number of integers. It provides a structured approach that minimizes the risk of errors.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful formula that connects the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
Let's find the GCD of 10 and 4 using the prime factorization method:
- Prime factorization of 10: 2 x 5
- Prime factorization of 4: 2 x 2 = 2²
The common prime factor is 2, and its lowest power is 2¹. Therefore, the GCD of 10 and 4 is 2.
Now, we can use the formula:
LCM(10, 4) x GCD(10, 4) = 10 x 4 LCM(10, 4) x 2 = 40 LCM(10, 4) = 40 / 2 LCM(10, 4) = 20
This method provides an alternative route to calculating the LCM, especially useful when the GCD is easily determined.
Understanding the Significance of LCM
The concept of LCM is far from being just an abstract mathematical concept. It has numerous practical applications in various fields:
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator, simplifying the calculation. For example, to add 1/4 and 1/10, we need to find the LCM of 4 and 10 (which is 20), making the calculation (5/20) + (2/20) = 7/20.
-
Scheduling and Timing: LCM is frequently used in scheduling problems. Imagine two buses leaving a station at different intervals. The LCM of their intervals will determine when they will depart at the same time again.
-
Cyclic Processes: In physics and engineering, many processes are cyclical in nature (e.g., rotating gears, oscillating systems). The LCM can help in determining the synchronization points of these processes.
-
Number Theory: LCM plays a vital role in number theory, providing essential tools for solving problems related to divisibility, prime numbers, and congruences.
Frequently Asked Questions (FAQ)
-
Q: Is the LCM always greater than the two numbers?
- A: Not always. If one number is a multiple of the other, the LCM is the larger number. For example, the LCM of 4 and 8 is 8.
-
Q: What if I have more than two numbers?
- A: The process of finding the LCM extends to more than two numbers. You can use prime factorization or the iterative method, finding the LCM of the first two, then the LCM of that result and the third number, and so on.
-
Q: Can the LCM of two numbers be the same as their product?
- A: Yes, this happens when the two numbers are coprime (meaning their GCD is 1). For example, the LCM of 10 and 9 is 90 (10 x 9).
-
Q: Are there any shortcuts for finding the LCM?
- A: For small numbers, the listing multiples method might be quicker. For larger numbers, prime factorization is generally more efficient. Using the GCD relationship can also be helpful.
Conclusion
Finding the least common multiple is a fundamental skill with far-reaching applications. This article explored three different methods for finding the LCM of 10 and 4, highlighting their strengths and weaknesses. Understanding the concept of LCM and its various methods equips you with a valuable tool for various mathematical challenges and practical problem-solving situations. Whether you are a student grappling with LCM problems, a teacher preparing lesson plans, or simply someone curious about this mathematical concept, this comprehensive guide should enhance your understanding and ability to determine LCMs efficiently. Remember to choose the method best suited to the specific problem at hand. Practice makes perfect, so apply these methods to different number pairs to solidify your understanding.
Latest Posts
Latest Posts
-
How To Calculate Solute Potential
Sep 14, 2025
-
Middle Eastern Countries And Capitals
Sep 14, 2025
-
What Is Informal Social Control
Sep 14, 2025
-
Rate Laws For Elementary Reactions
Sep 14, 2025
-
Model 2 Writing Electron Configuration
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.