Lcm Of 2 And 8
metako
Sep 18, 2025 · 6 min read
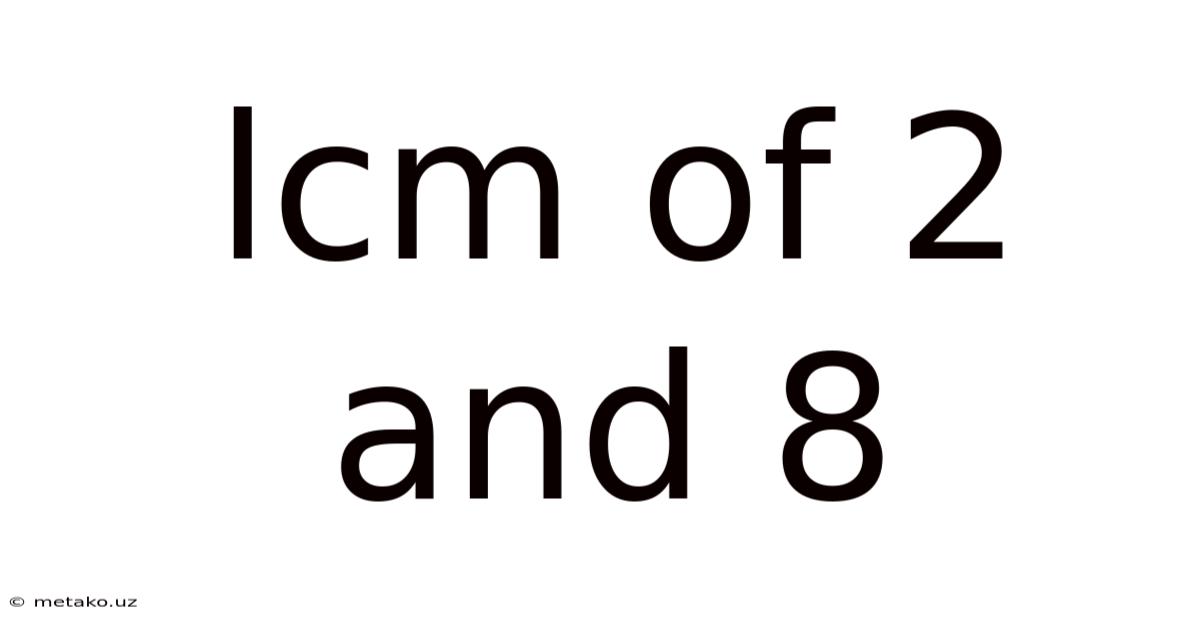
Table of Contents
Understanding the Least Common Multiple (LCM) of 2 and 8: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 2 and 8. However, understanding the underlying concepts and different methods for calculating the LCM is crucial for grasping more advanced mathematical concepts. This comprehensive guide will explore the LCM of 2 and 8, delving into various approaches, explaining the underlying theory, and providing practical applications. We'll move beyond a simple answer and explore the 'why' behind the calculations, making this concept clear for students of all levels.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding multiples is key here. A multiple of a number is the result of multiplying that number by any integer (whole number). For example, the multiples of 2 are 2, 4, 6, 8, 10, and so on.
Finding the LCM of 2 and 8: Method 1 - Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number and identifying the smallest common multiple.
Let's start with the multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
Now, let's list the multiples of 8: 8, 16, 24, 32, 40...
By comparing the two lists, we can see that the smallest number appearing in both lists is 8. Therefore, the LCM of 2 and 8 is 8.
This method is easy to visualize and understand, especially for smaller numbers. However, it becomes less practical when dealing with larger numbers or a greater number of integers.
Finding the LCM of 2 and 8: Method 2 - Prime Factorization
Prime factorization is a more powerful and efficient method for finding the LCM, particularly for larger numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime Factorization of 2: 2 (2 is itself a prime number)
- Prime Factorization of 8: 2 x 2 x 2 (or 2³)
Now, to find the LCM using prime factorization, we follow these steps:
- Identify the prime factors: We have only one prime factor: 2.
- Find the highest power of each prime factor: The highest power of 2 that appears in either factorization is 2³ (from the factorization of 8).
- Multiply the highest powers together: 2³ = 8
Therefore, the LCM of 2 and 8 is 8.
This method is more systematic and works effectively even with complex numbers and multiple integers. It avoids the cumbersome task of listing out all multiples.
Finding the LCM of 2 and 8: Method 3 - Using the Greatest Common Divisor (GCD)
The LCM and the Greatest Common Divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula that links the LCM and GCD:
LCM(a, b) * GCD(a, b) = a * b
where 'a' and 'b' are the two numbers.
Let's find the GCD of 2 and 8 first. The divisors of 2 are 1 and 2. The divisors of 8 are 1, 2, 4, and 8. The greatest common divisor is 2.
Now, we can use the formula:
LCM(2, 8) * GCD(2, 8) = 2 * 8 LCM(2, 8) * 2 = 16 LCM(2, 8) = 16 / 2 LCM(2, 8) = 8
This method demonstrates the interconnectedness of LCM and GCD, providing an alternative approach to calculating the LCM. It's particularly useful when dealing with larger numbers where finding the GCD might be easier than directly calculating the LCM.
Understanding the Concept of Multiples and Divisibility
Before moving on to more complex applications, let's solidify our understanding of multiples and divisibility.
- Multiples: A multiple of a number is the result of multiplying that number by any integer. For instance, the multiples of 3 are 3, 6, 9, 12, 15, and so on.
- Divisibility: A number is divisible by another number if it can be divided by that number without leaving a remainder. For example, 12 is divisible by 3 (12/3 = 4 with no remainder).
The concept of divisibility plays a crucial role in finding the LCM. The LCM must be divisible by all the numbers involved.
Real-World Applications of LCM
While finding the LCM of 2 and 8 might seem trivial, the concept of LCM has numerous practical applications in various fields:
- Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 2 hours, and the other every 8 hours. The LCM (8) tells us when both buses will arrive at the bus stop simultaneously.
- Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps to find a common denominator, making the calculation easier.
- Geometry: LCM is used in problems involving periodic patterns or repeating cycles in geometrical shapes.
- Music: In music theory, LCM is used to determine the least common multiple of the lengths of different musical phrases.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider all the prime factors of all the numbers and take the highest power of each. For the listing method, you would list the multiples of all numbers and find the smallest common multiple. The GCD method can also be extended using more sophisticated algorithms for finding the GCD of multiple numbers.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The Least Common Multiple (LCM) is the smallest number that is a multiple of all the given numbers. The Greatest Common Divisor (GCD) is the largest number that divides all the given numbers without leaving a remainder. They are inversely related; a higher GCD implies a lower LCM and vice-versa.
Q2: Is the LCM always larger than the numbers involved?
A2: Yes, the LCM will always be greater than or equal to the largest of the numbers involved. It will be equal only if one number is a multiple of the other (as in our example of 2 and 8).
Q3: How do I find the LCM of larger numbers?
A3: The prime factorization method is the most efficient for larger numbers. Using a calculator or software to find prime factors can simplify the process significantly.
Q4: Can I use a calculator to find the LCM?
A4: Yes, most scientific calculators and many online calculators have a built-in function to calculate the LCM of numbers.
Conclusion
Finding the LCM of 2 and 8, while seemingly simple, provides a foundational understanding of this important mathematical concept. Through different methods – listing multiples, prime factorization, and using the GCD – we have explored various approaches to calculate the LCM. Understanding these methods enables you to tackle more complex problems involving larger numbers and multiple integers. The LCM isn't just an abstract mathematical concept; it has significant practical applications in diverse fields, highlighting its relevance beyond the classroom. Mastering the LCM opens doors to a deeper comprehension of number theory and its applications in the real world. Remember, understanding the "why" behind the calculations is just as important as knowing the "how."
Latest Posts
Latest Posts
-
U Sub With Definite Integrals
Sep 18, 2025
-
Does An Electron Have Mass
Sep 18, 2025
-
How To Find Bond Angles
Sep 18, 2025
-
Difference Between Inheritance And Polymorphism
Sep 18, 2025
-
Cell Membrane And Transport Coloring
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.