Lcm Of 2 And 9
metako
Sep 17, 2025 · 6 min read
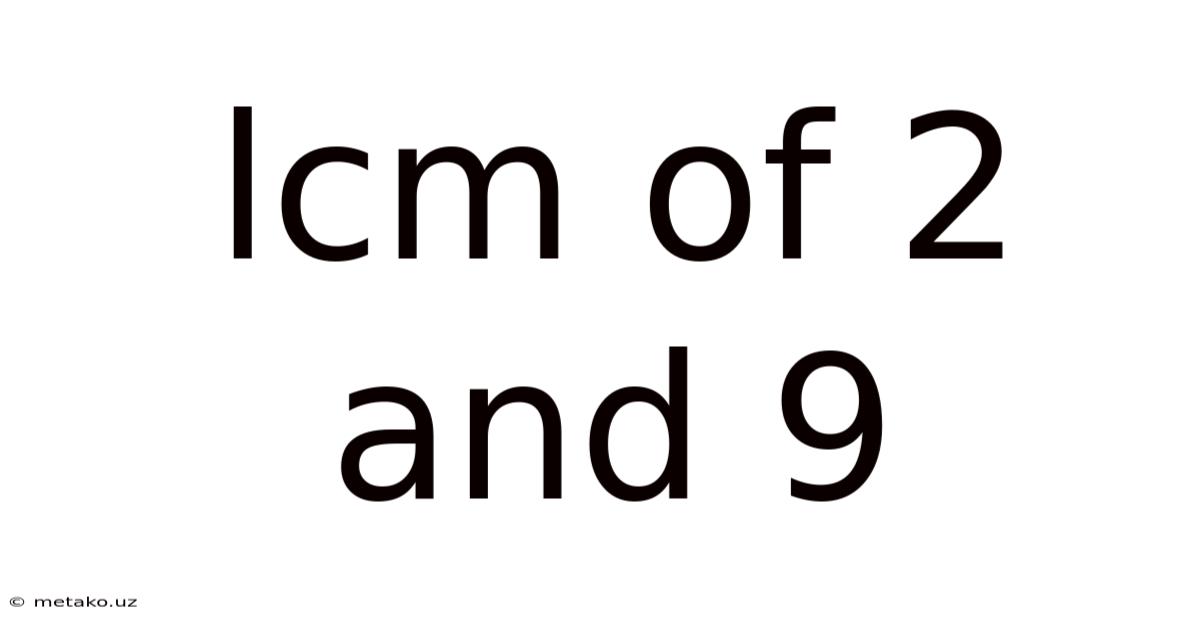
Table of Contents
Unveiling the Least Common Multiple (LCM) of 2 and 9: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but it underlies many fundamental concepts in mathematics and has practical applications in various fields. This article delves into the LCM of 2 and 9, exploring different methods to calculate it, explaining the underlying mathematical principles, and demonstrating its relevance in real-world scenarios. We'll also address frequently asked questions and provide further insights into the fascinating world of number theory.
Introduction: What is LCM?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. Understanding LCM is crucial in various mathematical operations, including fraction simplification, solving problems involving ratios and proportions, and even in more advanced areas like modular arithmetic and abstract algebra. This exploration will focus on finding the LCM of 2 and 9, using multiple approaches to solidify understanding.
Methods for Finding the LCM of 2 and 9
Several methods exist for determining the LCM of two numbers. We'll explore three common and effective approaches:
1. Listing Multiples Method:
This is a straightforward method, especially suitable for smaller numbers like 2 and 9. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 9: 9, 18, 27, 36, 45...
The smallest multiple that appears in both lists is 18. Therefore, the LCM of 2 and 9 is 18.
2. Prime Factorization Method:
This method uses the prime factorization of each number. The prime factorization is the representation of a number as a product of prime numbers (numbers divisible only by 1 and themselves).
- Prime factorization of 2: 2 (2 is a prime number itself)
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization:
- Identify all the prime factors that appear in either factorization. In this case, we have 2 and 3.
- For each prime factor, take the highest power that appears in any factorization. The highest power of 2 is 2¹, and the highest power of 3 is 3².
- Multiply these highest powers together: 2¹ x 3² = 2 x 9 = 18.
Therefore, the LCM of 2 and 9 is 18. This method is particularly useful for larger numbers where listing multiples becomes cumbersome.
3. Formula Method (using GCD):
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. There's a relationship between LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b (always positive).
Let's apply this to 2 and 9:
- Find the GCD of 2 and 9. The only common divisor of 2 and 9 is 1. Therefore, GCD(2, 9) = 1.
- Apply the formula: LCM(2, 9) = (|2 x 9|) / GCD(2, 9) = 18 / 1 = 18.
This confirms that the LCM of 2 and 9 is 18. This method is efficient for larger numbers, especially when using the Euclidean algorithm to find the GCD.
Explanation of the Mathematical Principles:
The LCM is fundamentally linked to the concept of divisibility. A number is divisible by another if the division results in a whole number (no remainder). Finding the LCM ensures we find the smallest number that satisfies the divisibility condition for all the given numbers. The prime factorization method highlights the building blocks of numbers and provides a structured approach to identify the smallest combination containing all necessary prime factors. The formula method illustrates a powerful relationship between LCM and GCD, emphasizing the interconnectedness of these fundamental number theory concepts.
Real-World Applications:
The concept of LCM finds numerous applications in everyday life and various fields:
-
Scheduling: Imagine two buses operating on different routes, one every 2 hours and the other every 9 hours. To determine when both buses will be at the starting point simultaneously, you need to find the LCM of 2 and 9, which is 18. Both buses will be at the starting point together every 18 hours.
-
Fraction Addition and Subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator. This allows for easier calculation.
-
Construction and Engineering: In construction, materials might be available in fixed lengths or quantities. Calculating the LCM ensures optimal material utilization by finding the smallest length that can be divided evenly among multiple requirements.
-
Music: Musical rhythms and harmonies often involve multiples of notes or beats. The LCM helps in determining when different rhythmic patterns will coincide or harmonize.
-
Computer Science: LCM is used in algorithms related to scheduling and resource management.
Frequently Asked Questions (FAQ):
-
Q: What is the difference between LCM and GCD?
- A: The LCM (Least Common Multiple) is the smallest number divisible by both given numbers, while the GCD (Greatest Common Divisor) is the largest number that divides both given numbers. They are inversely related; knowing one helps determine the other.
-
Q: Can the LCM of two numbers ever be smaller than the larger of the two numbers?
- A: Yes, this happens when the larger number is a multiple of the smaller number. For example, LCM(2, 4) = 4.
-
Q: How do I find the LCM of more than two numbers?
- A: You can extend the prime factorization method or use iterative applications of the LCM formula. Find the LCM of the first two numbers, then find the LCM of that result and the third number, and so on.
-
Q: What if one of the numbers is zero?
- A: The LCM is undefined if one of the numbers is zero because zero is not a positive integer and doesn't have positive multiples.
Conclusion:
Finding the least common multiple of 2 and 9, which is 18, illustrates fundamental concepts in number theory. The various methods presented – listing multiples, prime factorization, and using the GCD – provide different approaches to solve this problem and highlight the interconnectedness of mathematical concepts. Understanding LCM is essential not only for solving arithmetic problems but also for tackling real-world applications across various disciplines. This deep dive illuminates the importance of understanding fundamental mathematical concepts and their practical relevance in our world. The simplicity of this example with 2 and 9 belies the power and significance of LCM in more complex mathematical and practical scenarios. We hope this detailed exploration has not only provided the answer but also enriched your understanding of the LCM and its broader mathematical context.
Latest Posts
Latest Posts
-
Compare Contrast Cats And Dogs
Sep 17, 2025
-
Mean For Grouped Data Calculator
Sep 17, 2025
-
What Is The Weakest Acid
Sep 17, 2025
-
Endocrine System Worksheet With Answers
Sep 17, 2025
-
Is Hydrophilic Polar Or Nonpolar
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.