Lcm Of 24 And 36
metako
Sep 15, 2025 · 6 min read
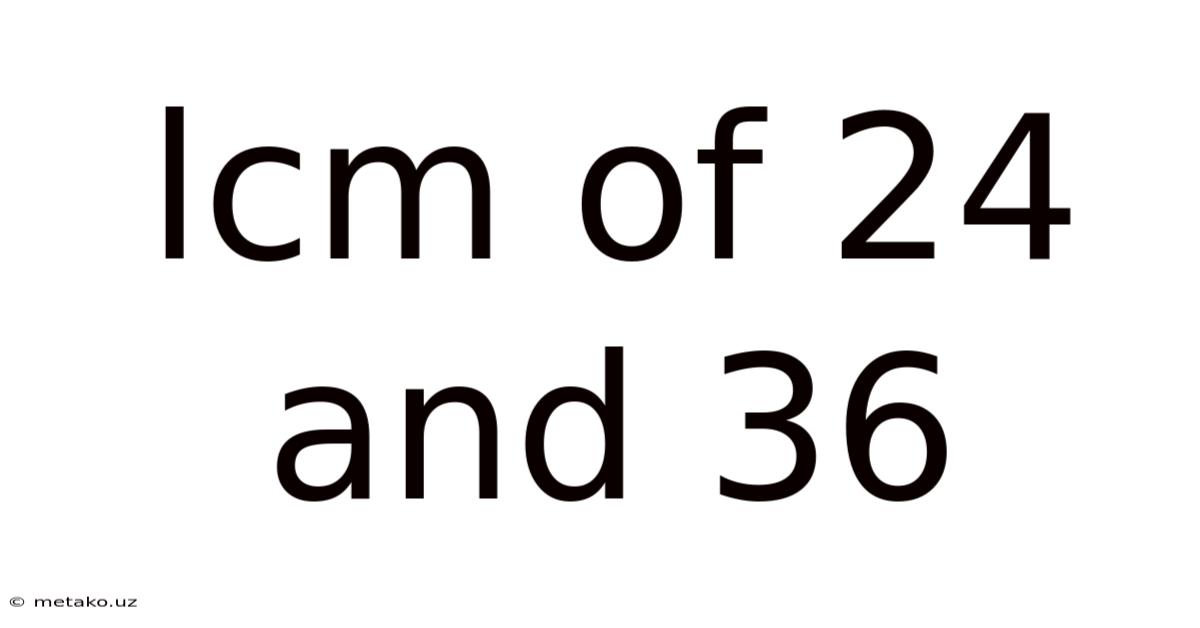
Table of Contents
Understanding the Least Common Multiple (LCM) of 24 and 36: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 24 and 36, might seem like a simple mathematical task. However, understanding the underlying concepts and various methods for calculating the LCM provides a strong foundation in number theory and its applications. This comprehensive guide will delve into the LCM of 24 and 36, explaining the process step-by-step, exploring different approaches, and addressing frequently asked questions. We'll go beyond a simple answer to build a robust understanding of this fundamental mathematical concept.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding LCM is crucial in various areas, from simplifying fractions and solving equations to scheduling events and understanding rhythmic patterns in music.
Methods for Finding the LCM of 24 and 36
There are several ways to calculate the LCM of 24 and 36. Let's explore three common methods:
1. Listing Multiples Method
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
- Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360...
By comparing the lists, we see that the smallest common multiple is 72. Therefore, the LCM(24, 36) = 72. This method is simple for smaller numbers, but becomes less efficient as the numbers increase.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization of a number is its expression as a product of prime numbers.
- Prime factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
- Prime factorization of 36: 36 = 2 x 2 x 3 x 3 = 2² x 3²
To find the LCM using prime factorization:
- Identify the highest power of each prime factor present in the factorizations. In this case, the highest power of 2 is 2³ and the highest power of 3 is 3².
- Multiply these highest powers together: 2³ x 3² = 8 x 9 = 72
Therefore, the LCM(24, 36) = 72. This method is generally more efficient than listing multiples, especially for larger numbers.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) = (a x b) / GCD(a, b)
First, let's find the GCD of 24 and 36 using the Euclidean algorithm:
- Divide the larger number (36) by the smaller number (24): 36 ÷ 24 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (24) and the smaller number with the remainder (12): 24 ÷ 12 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 12.
Now, we can use the formula:
LCM(24, 36) = (24 x 36) / GCD(24, 36) = (24 x 36) / 12 = 72
Therefore, the LCM(24, 36) = 72. This method is efficient and provides a deeper understanding of the relationship between LCM and GCD.
Real-World Applications of LCM
The concept of LCM extends beyond the realm of pure mathematics and finds practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 24 minutes, and the other every 36 minutes. The LCM (72 minutes) tells us when both buses will arrive at the stop simultaneously again.
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
-
Music Theory: The LCM is used in music to determine the least common period of two or more rhythmic patterns.
-
Construction and Engineering: In projects requiring repetitive patterns or cycles, LCM helps in optimizing resource allocation and scheduling.
-
Computer Science: In tasks involving synchronization of processes or data streams, the LCM is important for efficient scheduling and avoiding conflicts.
Beyond the Basics: Extending the Concept of LCM
The concept of LCM can be extended to more than two numbers. For instance, to find the LCM of 24, 36, and another number, say 18:
-
Prime Factorization:
- 24 = 2³ x 3¹
- 36 = 2² x 3²
- 18 = 2¹ x 3²
-
Highest Powers: The highest power of 2 is 2³, and the highest power of 3 is 3².
-
Multiplication: 2³ x 3² = 8 x 9 = 72. Therefore, LCM(24, 36, 18) = 72.
This shows that the LCM remains a valuable tool for dealing with multiple numbers simultaneously. The process remains the same: find the prime factorization of each number, identify the highest power of each prime factor present, and multiply these highest powers to obtain the LCM.
Frequently Asked Questions (FAQs)
Q1: What if the numbers have no common factors?
If two numbers are relatively prime (meaning their GCD is 1), then their LCM is simply the product of the two numbers. For example, LCM(5, 7) = 5 x 7 = 35.
Q2: Can the LCM of two numbers be smaller than either of the numbers?
No. The LCM of two numbers will always be greater than or equal to the larger of the two numbers. This is because the LCM must be a multiple of both numbers.
Q3: Are there any shortcuts for finding the LCM?
While the prime factorization and GCD methods are generally efficient, for very large numbers, more advanced algorithms might be used, but these are beyond the scope of this introductory guide. For smaller numbers, observing common multiples directly can be quicker.
Q4: What is the difference between LCM and GCD?
The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers, while the GCD (Greatest Common Divisor) is the largest number that divides both numbers without leaving a remainder. They are inversely related, as shown by the formula: LCM(a, b) = (a x b) / GCD(a, b).
Q5: How can I check if my calculated LCM is correct?
Verify that your calculated LCM is divisible by both original numbers without leaving a remainder. Also, try using a different method to calculate the LCM to confirm the result.
Conclusion
Understanding the least common multiple is a fundamental skill in mathematics with far-reaching applications. This guide has explored various methods for calculating the LCM of 24 and 36, demonstrating that the answer is 72. However, the true value lies in grasping the underlying principles and appreciating the diverse contexts in which this concept is applied. By mastering the LCM, you not only enhance your mathematical abilities but also develop a crucial tool for problem-solving in various real-world scenarios. Remember to practice different methods to solidify your understanding and choose the approach that best suits the given numbers and your level of mathematical comfort.
Latest Posts
Latest Posts
-
Polymer Molecular Weight Determination Methods
Sep 15, 2025
-
Unknown Lab Report For Microbiology
Sep 15, 2025
-
E Coli On Xld Agar
Sep 15, 2025
-
Non Verbal Communication In Psychotherapy
Sep 15, 2025
-
Path Function Vs State Function
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.