Lcm Of 24 And 40
metako
Sep 20, 2025 · 6 min read
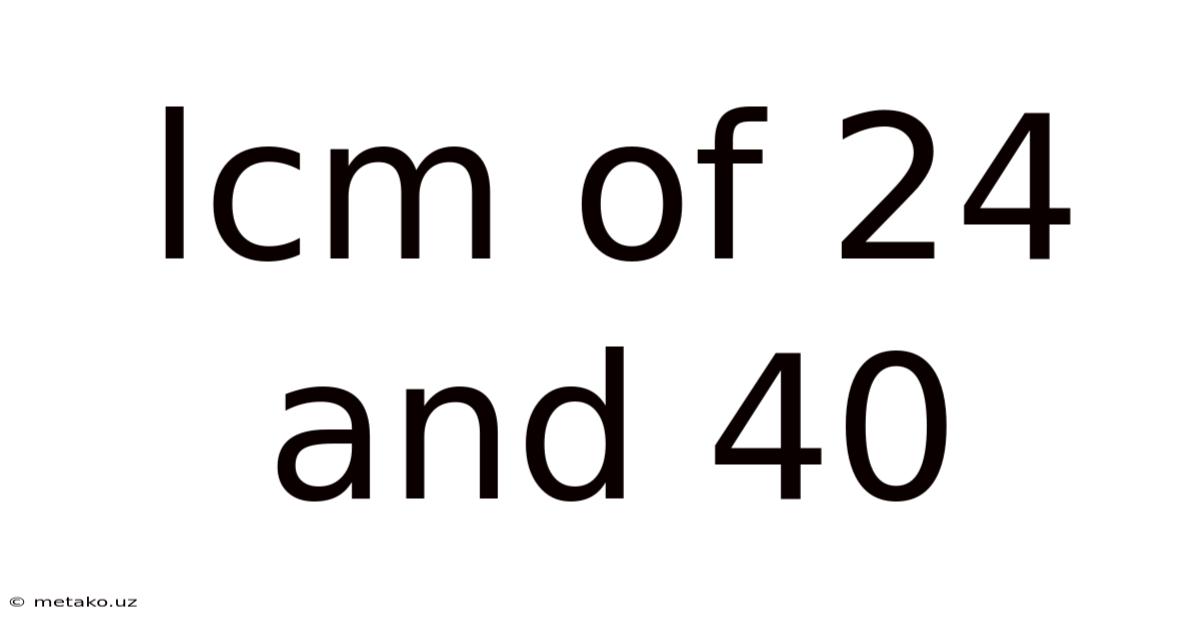
Table of Contents
Finding the Least Common Multiple (LCM) of 24 and 40: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, such as 24 and 40, might seem like a simple mathematical task. However, understanding the underlying principles and different methods for calculating the LCM opens doors to a deeper appreciation of number theory and its practical applications. This comprehensive guide will explore various approaches to finding the LCM of 24 and 40, delve into the mathematical concepts involved, and provide you with a solid foundation for tackling similar problems. We'll also explore why understanding LCM is crucial in various fields, from scheduling to construction.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers you're considering as factors. For instance, if we look at the multiples of 24 (24, 48, 72, 96, 120, 144...) and the multiples of 40 (40, 80, 120, 160...), we can see that 120 is the smallest number that appears in both lists. Therefore, the LCM of 24 and 40 is 120.
Method 1: Listing Multiples
The simplest method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168...
- Multiples of 40: 40, 80, 120, 160, 200...
As you can see, 120 is the smallest number that appears in both lists. This method is effective for small numbers but becomes cumbersome for larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves breaking down each number into its prime factors – the prime numbers that multiply together to give the original number.
-
Find the prime factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
-
Find the prime factorization of 40: 40 = 2 x 2 x 2 x 5 = 2³ x 5¹
-
Identify the highest power of each prime factor present in either factorization: The prime factors are 2, 3, and 5. The highest power of 2 is 2³ (8), the highest power of 3 is 3¹ (3), and the highest power of 5 is 5¹ (5).
-
Multiply the highest powers together: LCM(24, 40) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
This method is far more efficient than listing multiples, especially when dealing with larger numbers. It systematically accounts for all prime factors ensuring you find the smallest common multiple.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers themselves. This relationship provides an alternative method for finding the LCM.
-
Find the GCD of 24 and 40 using the Euclidean Algorithm:
- Divide the larger number (40) by the smaller number (24): 40 ÷ 24 = 1 with a remainder of 16.
- Replace the larger number with the smaller number (24) and the smaller number with the remainder (16): 24 ÷ 16 = 1 with a remainder of 8.
- Repeat the process: 16 ÷ 8 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 8.
-
Use the relationship between LCM and GCD:
LCM(a, b) = (a x b) / GCD(a, b)
LCM(24, 40) = (24 x 40) / 8 = 960 / 8 = 120
This method elegantly connects the LCM and GCD, providing a different perspective on their relationship and offering a potentially faster calculation, especially for larger numbers where finding prime factorizations can be more time-consuming.
The Importance of LCM in Real-World Applications
The concept of LCM isn't just a theoretical exercise; it has practical applications across various fields:
-
Scheduling: Imagine two buses depart from the same station, one every 24 minutes and the other every 40 minutes. The LCM (120 minutes, or 2 hours) tells you when both buses will depart simultaneously again. This concept extends to scheduling meetings, shifts, or any recurring events.
-
Construction and Engineering: When working with materials of different lengths, the LCM ensures efficient use of resources. For example, if you have tiles of length 24 cm and 40 cm, knowing the LCM (120 cm) allows you to determine the smallest length you can cover without cutting tiles. This minimizes waste and improves efficiency.
-
Music Theory: The LCM is used in music to determine the least common multiple of note durations, which is crucial for understanding rhythmic patterns and creating harmonious compositions.
-
Computer Science: LCM is utilized in algorithms and data structures to optimize processes or manage data efficiently. For instance, in finding the least common ancestor in a tree structure or synchronizing different threads.
-
Everyday Life: From cooking recipes that require different ingredient quantities, to scheduling household chores, LCM unconsciously helps us make efficient use of our time and resources.
Frequently Asked Questions (FAQs)
-
What if the numbers are very large? For very large numbers, the prime factorization method can become computationally intensive. In such cases, advanced algorithms and software tools are used to find the LCM efficiently.
-
Can the LCM be smaller than one of the numbers? No, the LCM is always greater than or equal to the largest of the two numbers.
-
What is the LCM of two numbers that are relatively prime (having a GCD of 1)? If two numbers are relatively prime (their GCD is 1), then their LCM is simply their product. For example, the LCM of 9 and 10 (which are relatively prime) is 90.
-
Is there a formula for calculating the LCM? Yes, as mentioned before, the formula based on the GCD is: LCM(a, b) = (a x b) / GCD(a, b)
-
Why is understanding LCM important? Understanding LCM helps optimize processes, improve efficiency, and solve practical problems in various fields, demonstrating the practical relevance of seemingly abstract mathematical concepts.
Conclusion
Finding the least common multiple of 24 and 40, while seemingly simple, highlights the beauty and utility of mathematical concepts. We explored multiple methods – listing multiples, prime factorization, and the GCD method – each with its strengths and weaknesses. Understanding these methods provides a solid foundation for tackling more complex LCM problems. The LCM is not just a theoretical concept; its applications across various fields underscore its practical significance in everyday life and professional settings. Mastering the concept of LCM empowers you to approach problems systematically and efficiently, highlighting the practical power of mathematical reasoning. So, next time you encounter a problem involving LCM, remember the various methods and apply the most appropriate one for the given context. The ability to find the LCM effectively demonstrates a deeper understanding of number theory and its relevance in the real world.
Latest Posts
Latest Posts
-
How To Identify Flint Rock
Sep 20, 2025
-
Ideal Gas Equation Practice Problems
Sep 20, 2025
-
How To Predict Chemical Reactions
Sep 20, 2025
-
London Dispersion Vs Dipole Dipole
Sep 20, 2025
-
Dim Of A Vector Space
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.