Lcm Of 3 And 12
metako
Sep 12, 2025 · 6 min read
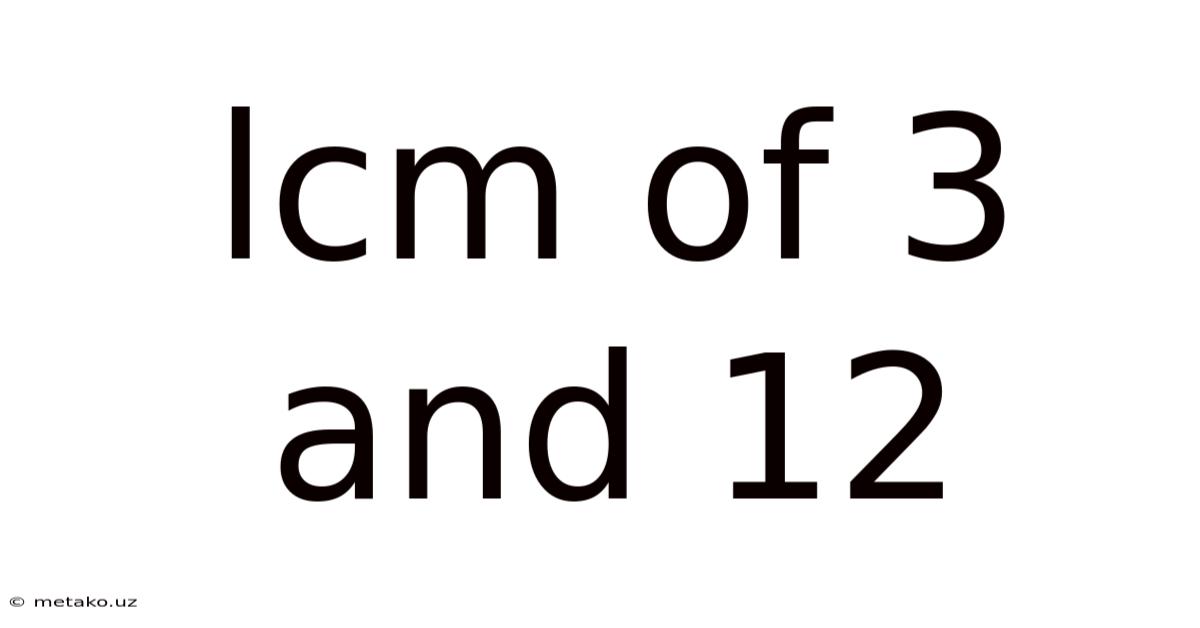
Table of Contents
Understanding the Least Common Multiple (LCM) of 3 and 12: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly important in areas like fractions, algebra, and even real-world problem-solving. This article provides a comprehensive exploration of how to find the LCM of 3 and 12, explaining various methods and delving into the underlying mathematical principles. We will cover different approaches, ensuring you understand not only the answer but also the 'why' behind the calculations. This will equip you with the skills to tackle similar LCM problems with confidence.
Introduction to Least Common Multiple (LCM)
Before diving into the specifics of finding the LCM of 3 and 12, let's define what a least common multiple is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors. Understanding this definition is crucial to grasping the concept and applying it effectively.
Method 1: Listing Multiples
The simplest method to find the LCM is by listing the multiples of each number until you find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
- Multiples of 12: 12, 24, 36, 48, 60…
By comparing the lists, we can see that the smallest number present in both lists is 12. Therefore, the LCM of 3 and 12 is 12. This method works well for smaller numbers but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
-
Prime Factorization of 3: 3 is a prime number, so its prime factorization is simply 3.
-
Prime Factorization of 12: 12 can be broken down as follows: 12 = 2 x 2 x 3 = 2² x 3
-
Finding the LCM: To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations of both numbers. In this case, we have:
- The prime factor 2 appears with the highest power of 2² in the factorization of 12.
- The prime factor 3 appears with the highest power of 3¹ in the factorization of both 3 and 12.
Therefore, the LCM is 2² x 3 = 4 x 3 = 12.
Method 3: Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the Greatest Common Divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
-
Finding the GCD of 3 and 12: The GCD of 3 and 12 is 3 because 3 is the largest number that divides both 3 and 12 evenly.
-
Using the Formula: There's a useful formula connecting the LCM and GCD of two numbers (a and b):
LCM(a, b) x GCD(a, b) = a x b
-
Applying the Formula: Substituting the values for 3 and 12:
LCM(3, 12) x GCD(3, 12) = 3 x 12 LCM(3, 12) x 3 = 36 LCM(3, 12) = 36 / 3 = 12
Why is the LCM Important?
Understanding and calculating the LCM is crucial in several mathematical contexts:
-
Adding and Subtracting Fractions: When adding or subtracting fractions with different denominators, you need to find the LCM of the denominators to create a common denominator. This allows you to perform the addition or subtraction accurately. For example, adding 1/3 and 1/12 requires finding the LCM of 3 and 12, which is 12. This allows you to rewrite the fractions as 4/12 and 1/12 respectively, easily adding them to get 5/12.
-
Solving Problems Involving Cycles or Periodic Events: The LCM is useful in problems involving events that repeat at regular intervals. For instance, if two buses depart from the same stop at different intervals, the LCM helps determine when they will depart together again.
-
Simplifying Algebraic Expressions: In algebra, the LCM is used to simplify expressions involving fractions and variables.
Illustrative Examples: Real-World Applications
Let's explore a couple of real-world scenarios where finding the LCM is beneficial:
Scenario 1: Baking: Imagine you're baking and need to use a recipe that requires you to measure out ingredients in multiples of 3 ounces and 12 ounces. To find the smallest amount of ingredients needed to use both measurements efficiently, without wasting any, you'd find the LCM of 3 and 12, which is 12 ounces.
Scenario 2: Scheduling: Let's say you have two tasks that need to be performed repeatedly: task A takes 3 days to complete, and task B takes 12 days. To determine when both tasks can be completed on the same day, again you need the LCM. The LCM of 3 and 12 is 12, meaning both tasks will complete on the same day after 12 days.
Frequently Asked Questions (FAQs)
Q1: What if I have more than two numbers? How do I find the LCM?
A1: The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you would consider all prime factors from all the numbers and take the highest power of each. For the GCD method, you would need to find the GCD of all the numbers and then use an iterative approach, finding the LCM of pairs and then incorporating additional numbers.
Q2: Is there a formula to directly calculate the LCM of any two numbers?
A2: While there isn't a single formula to directly calculate the LCM without involving prime factorization or GCD, the formula LCM(a, b) * GCD(a, b) = a * b is extremely helpful in finding the LCM once the GCD is known. Efficient algorithms for computing GCD, such as the Euclidean algorithm, exist and are implemented in programming languages and calculators.
Q3: How can I use a calculator or software to find the LCM?
A3: Most scientific calculators and mathematical software packages (like those found in many programming languages) have built-in functions or commands to calculate the LCM of numbers. Consult the documentation of your specific calculator or software for instructions.
Q4: Why is the LCM always greater than or equal to the largest number?
A4: The LCM must be divisible by both numbers. Since it's divisible by the larger number, it must be at least as large as that number. It might be larger if the numbers share common factors.
Conclusion
Finding the least common multiple is a valuable skill in mathematics with practical applications in various fields. This article has demonstrated three different methods for calculating the LCM, with a specific focus on finding the LCM of 3 and 12. By understanding these methods and their underlying principles, you can confidently tackle LCM problems of varying complexity. Remember to choose the method that best suits the numbers you're working with—listing multiples for small numbers, prime factorization for larger numbers, and the GCD method for efficiency when dealing with multiple numbers. The LCM is more than just a mathematical concept; it's a tool that helps us solve problems and understand the relationships between numbers in a more profound way.
Latest Posts
Latest Posts
-
Surface Area Of Parametric Surfaces
Sep 12, 2025
-
What Director Is Another Benzene
Sep 12, 2025
-
S3 2 Lewis Structure Resonance
Sep 12, 2025
-
Claim Of Policy Examples Brainly
Sep 12, 2025
-
Dissociation Of Acids And Bases
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.