Lcm Of 4 And 16
metako
Sep 20, 2025 · 5 min read
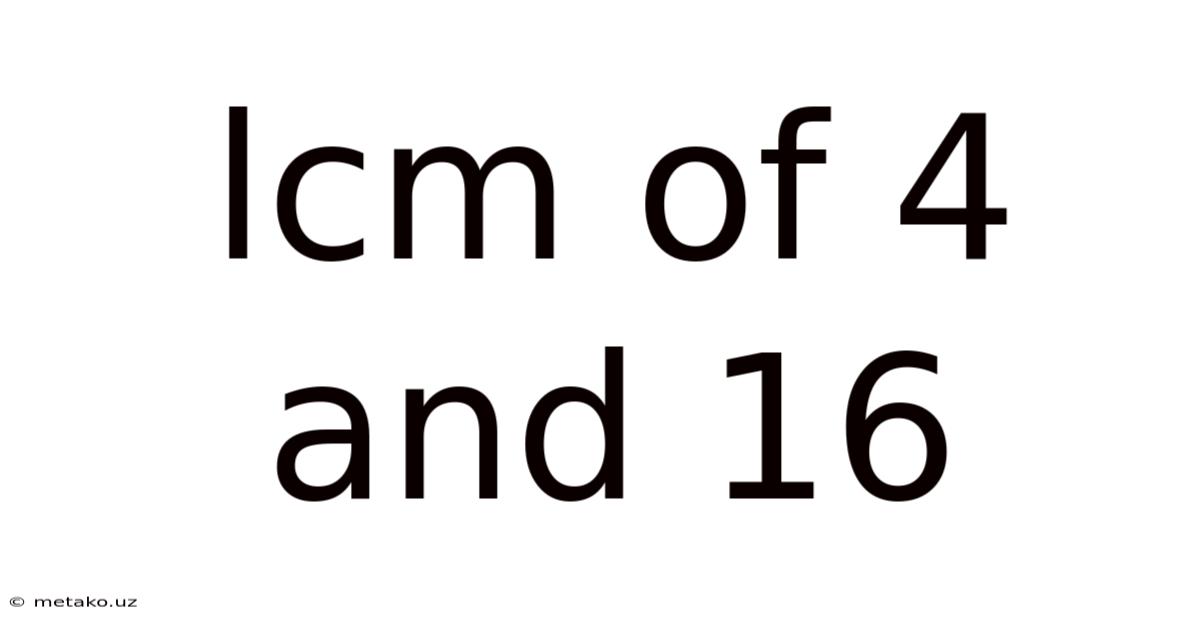
Table of Contents
Understanding the Least Common Multiple (LCM) of 4 and 16: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts provides a strong foundation for more advanced mathematics. This article delves deep into calculating the LCM of 4 and 16, exploring various methods and explaining the mathematical principles involved. We'll move beyond simply finding the answer and explore why this concept is crucial in various mathematical applications.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding this definition is key to grasping the entire concept.
Methods for Finding the LCM of 4 and 16
There are several effective methods to determine the LCM of 4 and 16. Let's explore the most common approaches:
1. Listing Multiples Method:
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
- Multiples of 16: 16, 32, 48, 64...
By comparing the lists, we quickly see that the smallest multiple common to both 4 and 16 is 16. Therefore, the LCM(4, 16) = 16.
This method is excellent for visualization and understanding the basic concept, but it can become less efficient with larger numbers.
2. Prime Factorization Method:
This method is more powerful and efficient, especially when dealing with larger numbers or finding the LCM of multiple numbers. It involves breaking down each number into its prime factors.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations. In this case, the only prime factor is 2, and its highest power is 2⁴.
Therefore, LCM(4, 16) = 2⁴ = 16.
3. Greatest Common Divisor (GCD) Method:
The LCM and GCD (Greatest Common Divisor) of two numbers are related through a simple formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 4 and 16. The GCD is the largest number that divides both 4 and 16 without leaving a remainder. In this case, the GCD(4, 16) = 4.
Now, we can use the formula:
LCM(4, 16) = (4 x 16) / 4 = 16
This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more challenging. The Euclidean algorithm is a highly efficient method for calculating the GCD.
Why is Finding the LCM Important?
The LCM isn't just an abstract mathematical concept; it has practical applications in various fields:
-
Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/4 and 3/16, we need to find the LCM of 4 and 16, which is 16. We then rewrite the fractions with a common denominator of 16 before adding them.
-
Scheduling: The LCM is used to solve scheduling problems. Imagine two events that repeat at different intervals. For example, Event A occurs every 4 days, and Event B occurs every 16 days. To find when both events occur on the same day, we need to find the LCM of 4 and 16, which is 16. Therefore, both events will occur together every 16 days.
-
Music: In music theory, the LCM helps determine the least common period of two or more rhythmic patterns. This is vital in composing music and understanding rhythmic relationships.
-
Modular Arithmetic: LCM plays a crucial role in solving problems related to modular arithmetic, a branch of number theory that deals with remainders after division.
-
Engineering and Construction: In engineering and construction projects, LCM can be used to synchronize repetitive tasks or processes which need to operate in a coordinated manner.
Expanding on the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly efficient for this purpose. Let's find the LCM of 4, 16, and 8:
- Prime factorization of 4: 2²
- Prime factorization of 16: 2⁴
- Prime factorization of 8: 2³
The highest power of 2 is 2⁴. Therefore, LCM(4, 16, 8) = 2⁴ = 16.
The Relationship Between LCM and GCD: A Deeper Dive
The relationship between the LCM and GCD is fundamental in number theory. For any two positive integers 'a' and 'b', the following equation always holds true:
LCM(a, b) * GCD(a, b) = a * b
This equation provides an alternative method for finding either the LCM or the GCD if the other is known.
Frequently Asked Questions (FAQ)
Q1: Is the LCM always greater than or equal to the largest of the given numbers?
A1: Yes. The LCM will always be at least as large as the largest number in the set because it must be divisible by the largest number.
Q2: What is the LCM of two numbers that are relatively prime (have no common factors other than 1)?
A2: If two numbers are relatively prime, their LCM is simply their product. For example, the LCM of 3 and 5 is 15 (3 x 5).
Q3: Can the LCM of two numbers be equal to one of the numbers?
A3: Yes. This happens when one number is a multiple of the other. For example, the LCM of 4 and 16 is 16.
Q4: How do I find the LCM of very large numbers?
A4: For very large numbers, using the prime factorization method can be computationally expensive. In such cases, algorithms like the Euclidean algorithm (for finding the GCD) combined with the formula relating LCM and GCD become more efficient.
Conclusion
Finding the least common multiple is a fundamental concept in mathematics with far-reaching applications. While seemingly simple for smaller numbers like 4 and 16, understanding the underlying principles and various methods allows you to tackle more complex problems involving larger numbers and multiple integers. Mastering this concept will significantly enhance your mathematical skills and provide you with a powerful tool to solve problems across various disciplines. Remember to choose the method most suited to the specific problem and always double-check your work for accuracy.
Latest Posts
Latest Posts
-
Is Soil A Pure Substance
Sep 20, 2025
-
Double Stem And Leaf Plot
Sep 20, 2025
-
Electric Field Ring Of Charge
Sep 20, 2025
-
Mixed Inhibitor Km And Vmax
Sep 20, 2025
-
P V Q Truth Table
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.