Lcm Of 7 And 8
metako
Sep 06, 2025 · 6 min read
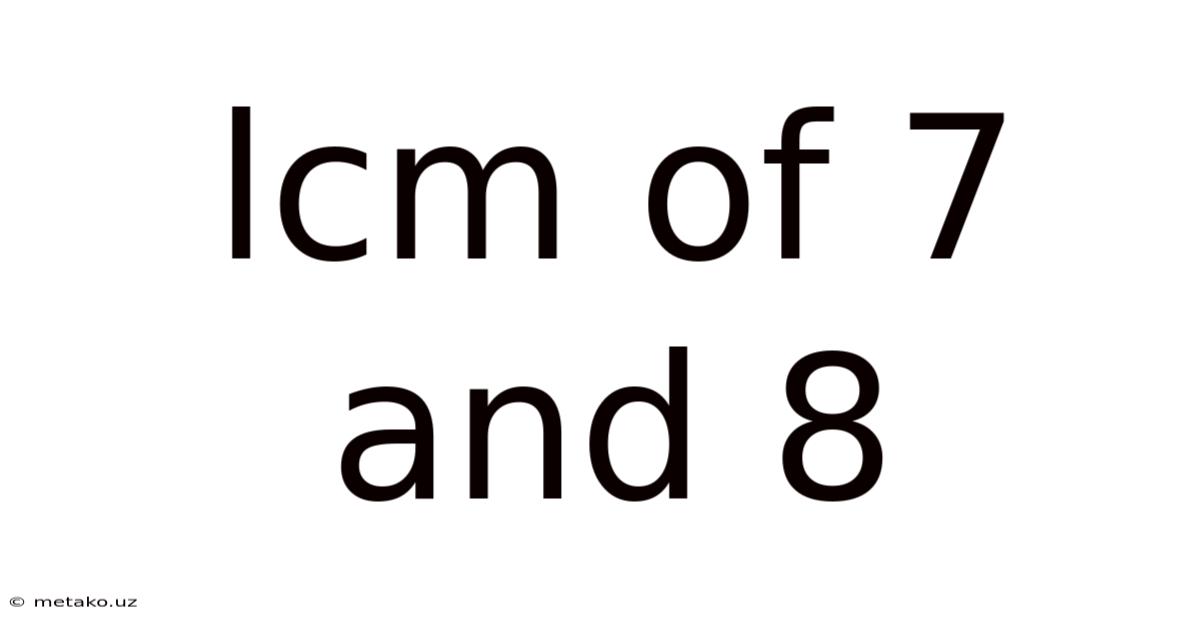
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 8: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation provides a strong foundation in number theory. This article delves deep into calculating the LCM of 7 and 8, explaining multiple approaches suitable for various levels of mathematical understanding. We’ll explore the prime factorization method, the listing multiples method, and the greatest common divisor (GCD) method, ensuring you grasp the core principles and can apply them to any pair of numbers. This comprehensive guide will equip you with the knowledge to confidently tackle LCM problems in your studies or everyday life.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 7 and 8, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Think of it like finding the smallest common "target" number that all the initial numbers can reach through multiplication.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is the smallest of these, which is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 7 and 8. We simply list out the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84…
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96…
By comparing the lists, we can see that the smallest number appearing in both lists is 56. Therefore, the LCM of 7 and 8 is 56.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
-
Find the prime factorization of each number:
- 7 is a prime number, so its prime factorization is simply 7.
- 8 can be factored as 2 x 2 x 2 = 2³
-
Identify the highest power of each prime factor:
- The prime factors involved are 2 and 7.
- The highest power of 2 is 2³ = 8.
- The highest power of 7 is 7¹ = 7.
-
Multiply the highest powers together:
- LCM(7, 8) = 2³ x 7 = 8 x 7 = 56
Method 3: Using the Greatest Common Divisor (GCD)
This method leverages the relationship between the LCM and the GCD (Greatest Common Divisor) of two numbers. The formula connecting LCM and GCD is:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
-
Find the GCD of 7 and 8:
Since 7 is a prime number and 8 is not divisible by 7, the GCD of 7 and 8 is 1. This means 7 and 8 share no common factors other than 1.
-
Apply the formula:
LCM(7, 8) = (7 x 8) / GCD(7, 8) = 56 / 1 = 56
Why is understanding LCM important?
The concept of LCM isn't just an abstract mathematical exercise; it has practical applications in various fields:
-
Scheduling: Imagine you have two events that occur at different intervals. The LCM helps determine when both events will coincide. For example, if one event happens every 7 days and another every 8 days, they will coincide again after 56 days.
-
Fractions: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
-
Measurement: When dealing with measurements using different units, LCM can help you find a common unit.
-
Geometry and Number Theory: LCM plays a vital role in various geometrical problems and advanced number theory concepts.
A Deeper Dive into Prime Factorization
The prime factorization method highlights a fundamental concept in number theory: the unique prime factorization theorem. This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This unique representation allows us to systematically find the LCM of any set of numbers. The process involves:
-
Finding the prime factors: This step often involves trial division, starting with the smallest prime number (2) and progressively testing for divisibility until you reach a prime factor.
-
Expressing the numbers in prime factor form: This involves writing each number as a product of its prime factors raised to appropriate powers. For example, 12 = 2² x 3¹.
-
Identifying the highest power of each prime factor: This step is crucial for finding the LCM. For each distinct prime factor present in the numbers, select the highest power found.
-
Multiplying the highest powers: The product of these highest powers gives the LCM.
Frequently Asked Questions (FAQ)
Q1: What if I have more than two numbers?
A1: The same methods can be extended to find the LCM of more than two numbers. For prime factorization, you would include all the prime factors from all the numbers and choose the highest power of each. For the listing multiples method, you would list multiples of all numbers until you find the smallest common multiple. The GCD method can be extended using more sophisticated algorithms.
Q2: Is there a shortcut for finding the LCM?
A2: While the prime factorization method is often efficient, there isn't a universal "shortcut" that always works better. For small numbers, the listing method is quick. For larger numbers, the prime factorization or GCD method is more practical and less prone to error.
Q3: What if one of the numbers is 0?
A3: The LCM of any number and 0 is undefined. The concept of multiples doesn't apply to 0.
Conclusion
Calculating the LCM of 7 and 8, as demonstrated through various methods, provides a solid understanding of fundamental number theory concepts. The choice of method depends on the context and the numbers involved. While the listing multiples method offers a simple visual approach for smaller numbers, the prime factorization and GCD methods are more efficient and reveal deeper mathematical relationships, paving the way for tackling more complex problems. Mastering LCM calculation strengthens your foundational mathematical skills, proving useful in various academic and practical scenarios. Remember to choose the method best suited to the problem at hand, and don't hesitate to revisit these different approaches to solidify your understanding.
Latest Posts
Latest Posts
-
High Spin And Low Spin
Sep 06, 2025
-
Ir Ranges For Functional Groups
Sep 06, 2025
-
What Controls Transcription In Prokaryotes
Sep 06, 2025
-
Mendels Plant Experiments Demonstrated That
Sep 06, 2025
-
Electrophilic Addition To Conjugated Dienes
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.