Lcm Of 8 And 18
metako
Sep 20, 2025 · 6 min read
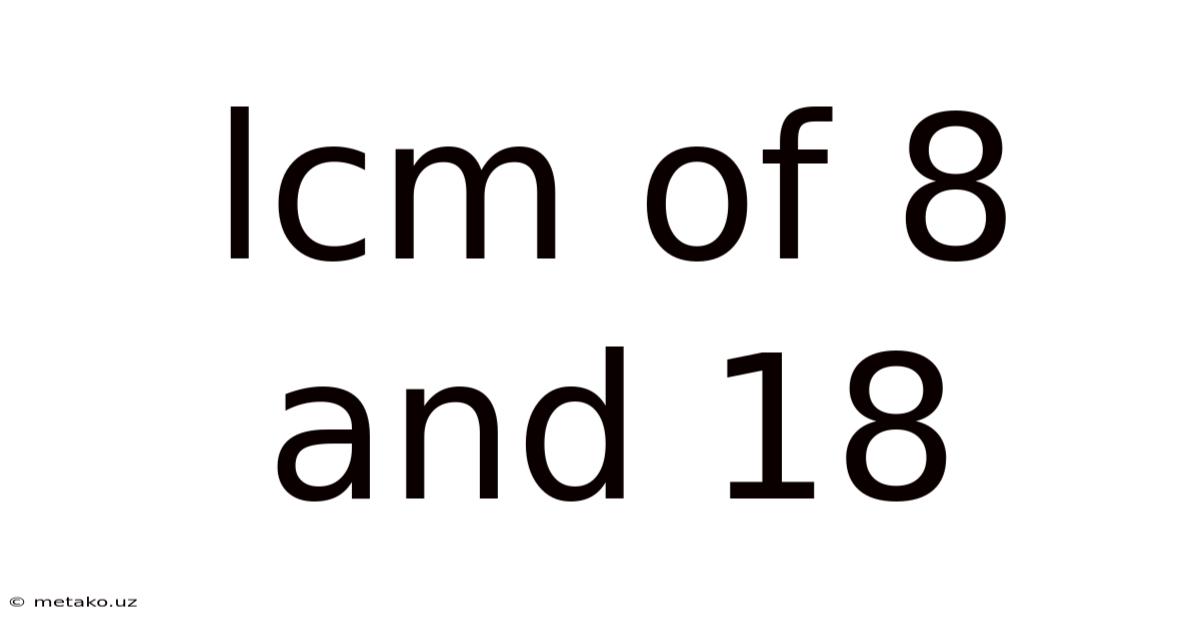
Table of Contents
Finding the Least Common Multiple (LCM) of 8 and 18: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for solving problems in various fields, from fractions and ratios to scheduling and music theory. This comprehensive guide will delve into the process of calculating the LCM of 8 and 18, exploring multiple methods and providing a deeper understanding of the underlying mathematical principles. We'll cover different approaches, ensuring you're equipped to tackle similar problems with confidence.
Understanding Least Common Multiples
Before we dive into the calculation, let's clarify what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that both numbers can divide into evenly. For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest, albeit less efficient for larger numbers, method is to list the multiples of each number until you find the smallest common multiple. Let's apply this to 8 and 18:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 18: 18, 36, 54, 72, 90...
Notice that the smallest number that appears in both lists is 72. Therefore, the LCM of 8 and 18 is 72. This method is suitable for smaller numbers but becomes cumbersome as the numbers increase in size.
Method 2: Prime Factorization
A more efficient and mathematically robust method involves prime factorization. This method breaks down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's factorize 8 and 18:
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(8, 18) = 2³ x 3² = 8 x 9 = 72
This method is far more efficient, especially when dealing with larger numbers or multiple numbers. It provides a systematic approach that avoids the tedious listing of multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula connecting the LCM and GCD:
LCM(a, b) = (a x b) / GCD(a, b)
First, let's find the GCD of 8 and 18 using the Euclidean algorithm:
- Divide the larger number (18) by the smaller number (8): 18 = 2 x 8 + 2
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (2): 8 = 4 x 2 + 0
- The GCD is the last non-zero remainder, which is 2.
Now, we can use the formula:
LCM(8, 18) = (8 x 18) / 2 = 144 / 2 = 72
This method elegantly connects the concepts of LCM and GCD, offering another efficient pathway to the solution. The Euclidean algorithm is particularly useful for finding the GCD of larger numbers.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method offers a deeper understanding of the mathematical underpinnings of LCM calculations. The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This unique representation allows us to systematically determine the LCM by considering the highest power of each prime factor present.
Understanding prime factorization is crucial not only for finding LCMs but also for simplifying fractions, solving Diophantine equations, and various other mathematical applications. It highlights the building blocks of numbers and how they combine to form larger integers.
The prime factorization of a number reveals valuable information about its divisibility properties. For instance, knowing the prime factors of a number allows us to easily determine if it's divisible by a specific prime number or a combination of prime numbers.
Let's consider a more complex example: Finding the LCM of 24, 36, and 60.
-
Prime Factorization:
- 24 = 2³ x 3
- 36 = 2² x 3²
- 60 = 2² x 3 x 5
-
Identifying Highest Powers: The highest powers of the prime factors are 2³, 3², and 5.
-
Calculating the LCM: LCM(24, 36, 60) = 2³ x 3² x 5 = 8 x 9 x 5 = 360
This demonstrates the power and efficiency of the prime factorization method, even when dealing with multiple numbers.
Applications of LCM in Real-World Scenarios
The concept of LCM extends beyond abstract mathematical exercises. It has practical applications in various real-world situations:
-
Scheduling: Imagine you have two machines that perform a specific task. One machine takes 8 hours to complete the task, and the other takes 18 hours. To determine when both machines will finish their tasks simultaneously, you need to find the LCM(8, 18) = 72. This means both machines will complete the task simultaneously after 72 hours.
-
Fractions: When adding or subtracting fractions with different denominators, you need to find the LCM of the denominators to determine the least common denominator (LCD). This allows you to rewrite the fractions with a common denominator, simplifying the addition or subtraction.
-
Music Theory: LCM plays a role in music theory when dealing with rhythms and time signatures. Finding the LCM of different note durations helps in determining the smallest common time interval for musical phrases.
-
Gear Ratios: In mechanical engineering, LCM is used to calculate gear ratios to optimize the speed and torque transmission in machinery.
Frequently Asked Questions (FAQ)
Q: What if one of the numbers is 0?
A: The LCM of any number and 0 is undefined. Zero has infinitely many multiples, making it impossible to determine a least common multiple.
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, this happens if one number is a multiple of the other. For example, LCM(4, 8) = 8.
Q: Is there a method to find the LCM of more than two numbers?
A: Yes, the prime factorization method readily extends to more than two numbers. You simply find the prime factorization of each number, identify the highest power of each distinct prime factor, and then multiply these highest powers together to find the LCM.
Conclusion
Finding the least common multiple of 8 and 18, or any set of numbers, is a fundamental skill with wide-ranging applications. While the method of listing multiples is straightforward for smaller numbers, the prime factorization method provides a more efficient and mathematically insightful approach, particularly for larger numbers. Understanding the relationship between LCM and GCD provides an alternative pathway for calculation. Mastering these methods equips you not only to solve mathematical problems but also to tackle real-world scenarios that require the determination of the least common multiple. Remember the power of prime factorization – it's the key to unlocking many mathematical concepts and their applications. By understanding the underlying principles, you can confidently tackle more complex LCM problems and appreciate the elegance and utility of this essential mathematical concept.
Latest Posts
Latest Posts
-
Similarities Between Fission And Fusion
Sep 20, 2025
-
Mitosis And Meiosis Venn Diagram
Sep 20, 2025
-
Is Sucrose Polar Or Nonpolar
Sep 20, 2025
-
Manganese Dioxide And Hydrogen Peroxide
Sep 20, 2025
-
Baltimore Classification Of Viruses Table
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.