Power Series For 1 X
metako
Sep 18, 2025 · 7 min read
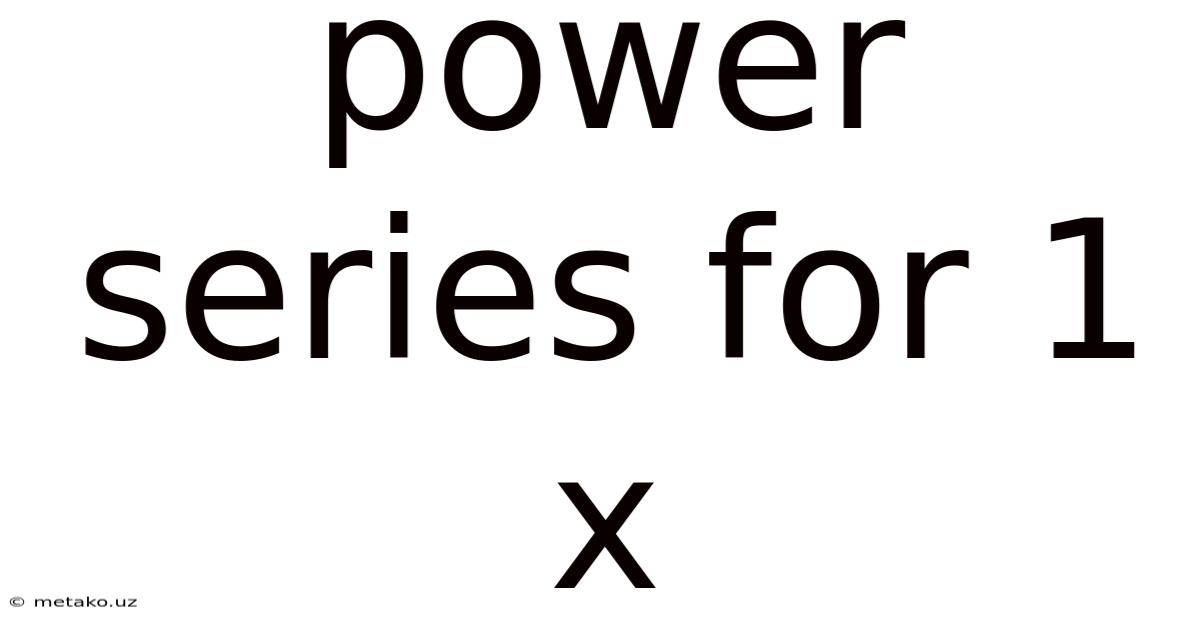
Table of Contents
Power Series Representation of 1/(1-x) and its Applications
The function 1/(1-x) holds a special place in mathematics, particularly in the realm of calculus and analysis. Its power series representation, a cornerstone of many mathematical concepts, provides a powerful tool for approximating functions, solving differential equations, and understanding complex phenomena. This article will delve into the derivation, properties, and applications of the power series for 1/(1-x), exploring its significance in a clear and accessible manner. We'll uncover why this seemingly simple function is so incredibly useful and impactful.
Understanding Power Series
Before diving into the specifics of 1/(1-x), let's establish a foundational understanding of power series. A power series is an infinite sum of the form:
∑<sub>n=0</sub><sup>∞</sup> a<sub>n</sub>(x - c)<sup>n</sup> = a<sub>0</sub> + a<sub>1</sub>(x - c) + a<sub>2</sub>(x - c)<sup>2</sup> + ...
where:
- a<sub>n</sub> are constants called coefficients.
- x is a variable.
- c is a constant called the center of the series.
The power series converges for some values of x and diverges for others. The set of x values for which the series converges is called the interval of convergence, and the radius of convergence, denoted by R, determines the size of this interval.
Deriving the Power Series for 1/(1-x)
There are several ways to derive the power series for 1/(1-x). One of the most straightforward methods uses the geometric series formula. Recall the formula for the sum of a finite geometric series:
S<sub>n</sub> = a(1 - r<sup>n</sup>) / (1 - r)
where:
- a is the first term.
- r is the common ratio.
- n is the number of terms.
If |r| < 1, as n approaches infinity, r<sup>n</sup> approaches 0, and the sum converges to:
S = a / (1 - r)
Now, consider the function 1/(1-x). We can rewrite this as:
1/(1-x) = 1 + x + x<sup>2</sup> + x<sup>3</sup> + ...
This is a geometric series with a = 1 and r = x. This series converges if |x| < 1. Therefore, the power series representation of 1/(1-x) is:
1/(1-x) = ∑<sub>n=0</sub><sup>∞</sup> x<sup>n</sup> for |x| < 1
Interval and Radius of Convergence
As mentioned earlier, the power series converges only when |x| < 1. This is the interval of convergence, specifically (-1, 1). The radius of convergence is R = 1. At the endpoints x = 1 and x = -1, the series diverges. Let's examine why:
- x = 1: The series becomes 1 + 1 + 1 + 1 + ..., which clearly diverges (it's an infinite sum of 1s).
- x = -1: The series becomes 1 - 1 + 1 - 1 + ..., which also diverges (it oscillates between 1 and 0).
Applications of the Power Series for 1/(1-x)
The power series for 1/(1-x) is not merely a theoretical curiosity; it has far-reaching applications across various fields:
1. Approximating Functions: The power series provides a way to approximate the value of 1/(1-x) for values of x within the interval of convergence. The more terms you include in the summation, the more accurate the approximation becomes. This technique is crucial in numerical analysis and computer science, where precise calculations are often impossible or computationally expensive.
2. Solving Differential Equations: Many differential equations can be solved using power series methods. The power series for 1/(1-x) often serves as a building block in these solutions. By expressing a solution as a power series and substituting it into the differential equation, we can determine the coefficients of the series and obtain the solution.
3. Generating Functions: In combinatorics and probability theory, power series are often used as generating functions. The power series for 1/(1-x) is a fundamental example. It can be used to derive formulas for various combinatorial quantities, such as the number of ways to choose k items from a set of n items (binomial coefficients).
4. Calculus and Analysis: The power series provides a powerful tool for understanding the behavior of functions. For instance, it can be used to find derivatives and integrals of functions. The derivative of 1/(1-x) can be easily obtained by differentiating the power series term by term within the interval of convergence. This method avoids the more complex quotient rule.
5. Physics and Engineering: Power series are frequently employed in physics and engineering to model and analyze various phenomena. The power series for 1/(1-x) can appear in solutions to problems involving oscillations, heat transfer, and other physical processes.
6. Derivation of other Power Series: By manipulating the power series for 1/(1-x), we can derive the power series representation for other functions. For example, by substituting -x for x, we get the power series for 1/(1+x). Integration and differentiation of this series can then yield power series for functions like ln(1+x) and arctan(x).
Beyond the Basic Series: Modifications and Extensions
The power series representation for 1/(1-x) forms the basis for numerous other important power series expansions. Here are a few key examples:
-
1/(1+x): By replacing x with -x in the original series, we obtain:
1/(1+x) = ∑<sub>n=0</sub><sup>∞</sup> (-x)<sup>n</sup> = ∑<sub>n=0</sub><sup>∞</sup> (-1)<sup>n</sup>x<sup>n</sup> for |x| < 1
-
ln(1+x): Integrating the power series for 1/(1+x) term by term yields the power series for ln(1+x):
ln(1+x) = ∑<sub>n=1</sub><sup>∞</sup> (-1)<sup>n+1</sup>x<sup>n</sup>/n for -1 < x ≤ 1
-
(1+x)<sup>k</sup> (Binomial Theorem): The binomial theorem generalizes to non-integer exponents using a power series:
(1+x)<sup>k</sup> = ∑<sub>n=0</sub><sup>∞</sup> (k choose n) x<sup>n</sup> where (k choose n) = k(k-1)...(k-n+1)/n! for |x|<1
This expression is particularly useful for values of k that are not positive integers, allowing approximation of non-integer powers.
Frequently Asked Questions (FAQ)
Q: What happens if |x| ≥ 1?
A: The power series diverges for |x| ≥ 1. The geometric series formula only holds when the absolute value of the common ratio (x in this case) is less than 1.
Q: Why is the interval of convergence (-1, 1] for ln(1+x) and not just (-1,1)?
A: The integral of 1/(1+x) which yields ln(1+x) converges at x = 1 (Alternating Series Test). This is a subtle but important point demonstrating the potential differences between the convergence of the original series and its integral.
Q: Can we use this power series to approximate 1/(1-2)?
A: No. The value of x (2 in this case) falls outside the interval of convergence (-1, 1). Therefore, the power series is not valid for this approximation.
Q: How accurate is the approximation using the power series?
A: The accuracy increases as more terms are included in the summation. The error of the approximation can be bounded using techniques from calculus, such as the remainder term in Taylor's theorem.
Conclusion
The power series representation of 1/(1-x) is a fundamental concept with far-reaching implications in mathematics and its applications. Its simplicity belies its power, enabling approximation, problem-solving, and theoretical understanding in diverse fields. By understanding its derivation, properties, and applications, you gain a crucial tool for tackling complex mathematical and scientific challenges. From approximating function values to solving differential equations and understanding complex phenomena, the power series for 1/(1-x) remains a vital and indispensable component of higher mathematics. Its ability to be manipulated and extended to derive other crucial power series underscores its central role in the mathematical landscape.
Latest Posts
Latest Posts
-
Multiplication Of Rational Algebraic Expression
Sep 18, 2025
-
Is Tap Water A Compound
Sep 18, 2025
-
Is Gravity A Conservative Force
Sep 18, 2025
-
Difference Between Inter And Intramolecular
Sep 18, 2025
-
What Is A Solution Biology
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Power Series For 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.