The Square Root Of 225
metako
Sep 18, 2025 · 6 min read
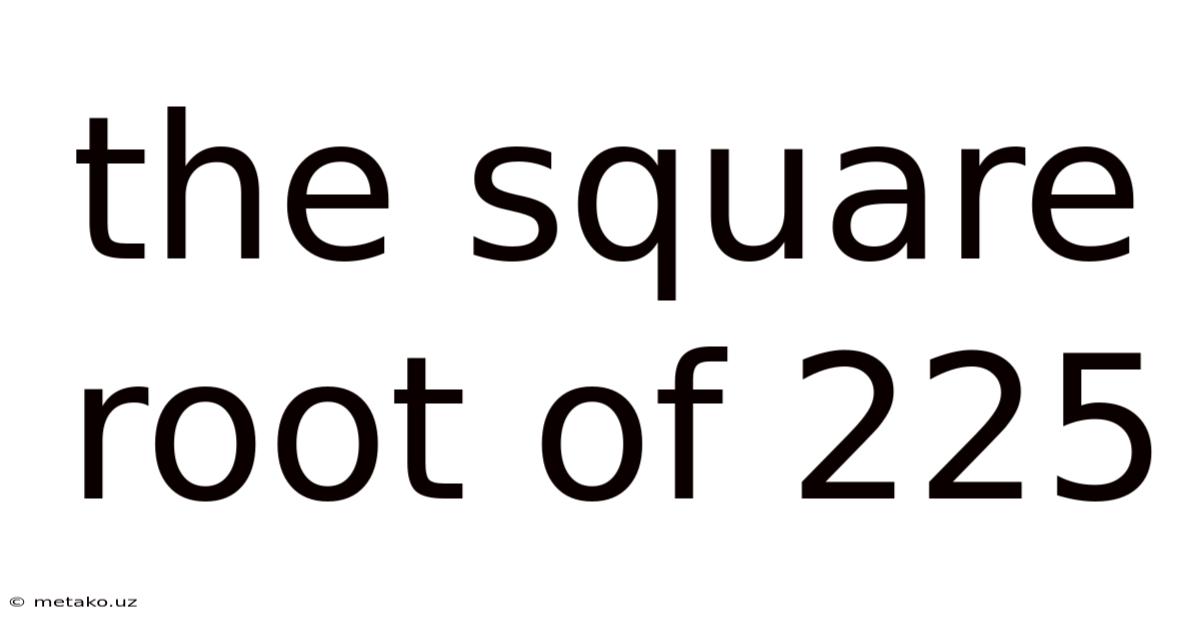
Table of Contents
Unveiling the Mystery: A Deep Dive into the Square Root of 225
Finding the square root of a number might seem like a simple mathematical task, especially for smaller numbers. But even seemingly straightforward calculations can reveal fascinating insights into the world of mathematics. This article delves into the square root of 225, exploring not just the answer but also the underlying concepts, methods of calculation, and its applications in various fields. Understanding the square root of 225 provides a stepping stone to grasping more complex mathematical concepts. This exploration will be particularly beneficial for students learning about square roots, radicals, and basic algebra.
What is a Square Root?
Before we dive into the specifics of the square root of 225, let's clarify the fundamental concept. A square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3, because 3 x 3 = 9. It's denoted by the symbol √. Every positive number has two square roots: a positive and a negative one. However, when we talk about "the" square root, we generally refer to the principal square root, which is the positive one.
Calculating the Square Root of 225: Different Approaches
There are several ways to calculate the square root of 225. Let's explore a few:
1. Prime Factorization:
This method is particularly useful for larger numbers. We break down 225 into its prime factors:
225 = 3 x 75 = 3 x 3 x 25 = 3 x 3 x 5 x 5 = 3² x 5²
Since the square root involves finding a number that, when multiplied by itself, equals the original number, we can simplify this:
√225 = √(3² x 5²) = √3² x √5² = 3 x 5 = 15
Therefore, the square root of 225 is 15.
2. Using a Calculator:
The most straightforward method, especially for larger numbers, is to use a calculator. Simply enter 225 and press the square root button (√). The calculator will quickly provide the answer: 15.
3. Estimation and Iteration (Newton-Raphson Method):
For those who enjoy a more hands-on approach, iterative methods can be used. The Newton-Raphson method is a powerful technique for approximating square roots. While this method is generally used for more complex calculations, it can be applied to 225 for illustrative purposes. It involves starting with an initial guess and repeatedly refining it using a specific formula. This method is beyond the scope of a basic explanation of the square root of 225, but it's worth noting its existence for more advanced learners.
4. Recognizing Perfect Squares:
This method relies on familiarity with perfect squares. A perfect square is a number that is the square of an integer. With practice, you can quickly recognize that 15 x 15 = 225. This makes 15 the square root of 225. This method becomes faster with increased exposure to perfect squares.
The Significance of 15: Beyond the Calculation
The result, 15, is more than just a numerical answer. It represents a point of intersection between various mathematical concepts. It's a composite number (meaning it has factors other than 1 and itself), and it's divisible by 3 and 5. Understanding its factors helps us further appreciate the prime factorization method described earlier. Furthermore, 15 appears in various mathematical sequences and patterns, adding to its significance within the broader context of number theory.
Applications of Square Roots and the Square Root of 225 in Real-World Scenarios
The concept of square roots, and hence the square root of 225, finds its way into various practical applications:
-
Geometry: Calculating the side length of a square given its area. If a square has an area of 225 square units, its side length is √225 = 15 units. This principle extends to calculating distances and dimensions in various geometric shapes.
-
Physics: Many physics equations involve square roots. For instance, calculating the velocity of an object using the formula relating kinetic energy and mass employs square roots. While the square root of 225 might not directly appear in such equations in common physics problems, the concept is fundamentally important.
-
Engineering: Engineering designs often utilize square roots in calculations related to structural stability, power systems, and signal processing. Understanding and efficiently computing square roots is crucial for precise calculations.
-
Finance: Calculating compound interest often involves square roots, particularly when dealing with present and future values of investments.
-
Computer Science: Algorithms in computer science often incorporate square root calculations for tasks like image processing, data analysis, and searching.
Understanding Radicals and Their Properties
The square root symbol (√) is a type of radical. Radicals represent roots of numbers. A radical expression contains a radical symbol, a radicand (the number inside the radical), and an index (the degree of the root). For square roots, the index is 2 (implied, not usually written).
Understanding the properties of radicals is crucial for manipulating and simplifying radical expressions. These properties include:
- Product Property: √(a x b) = √a x √b
- Quotient Property: √(a/b) = √a / √b
- Simplifying Radicals: Removing perfect square factors from the radicand.
These properties can be applied to manipulate and simplify expressions involving the square root of 225 and other radical expressions.
Frequently Asked Questions (FAQs)
Q1: Is there a negative square root of 225?
A1: Yes, the negative square root of 225 is -15, because (-15) x (-15) = 225. However, the principal square root (the one typically referred to) is the positive value, 15.
Q2: How can I estimate the square root of a number without a calculator?
A2: For numbers close to perfect squares, you can estimate. For instance, knowing that 15² = 225 and 16² = 256, you can quickly deduce that √225 is slightly less than 16 and, indeed, is 15. More complex estimation techniques exist for numbers further from perfect squares.
Q3: Are there any real-world applications of the square root of 225 specifically?
A3: While there aren't specific real-world applications solely involving the square root of 225, the concept is crucial in many applications as discussed previously. A 15-meter side length of a square, area calculation in construction, or a velocity calculation may utilize it as part of a broader calculation.
Q4: What if I need to find the cube root (or higher roots) of 225?
A4: Finding the cube root (∛) involves finding a number that, when multiplied by itself three times, equals the original number. The cube root of 225 is approximately 6.08, and it’s not a whole number. Calculating higher roots requires more advanced methods or calculators.
Conclusion
The seemingly simple calculation of the square root of 225 opens doors to a wider understanding of mathematical concepts, from prime factorization and perfect squares to the practical applications of square roots in various fields. This exploration underscores the importance of understanding not just the answer but also the underlying principles and methods involved in reaching that answer. This deeper understanding empowers individuals to tackle more complex mathematical problems and appreciate the interconnectedness of mathematical concepts in the real world. The journey from finding a simple square root to grasping its broader implications showcases the beauty and power of mathematical exploration.
Latest Posts
Latest Posts
-
What Is Qrev In Chemistry
Sep 18, 2025
-
One Common Trait Of Monoplacophora
Sep 18, 2025
-
Kirby Bauer Disk Diffusion Test
Sep 18, 2025
-
How To Solve Line Integrals
Sep 18, 2025
-
Is Sio2 Soluble In Water
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about The Square Root Of 225 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.