V Lwh Solve For H
metako
Sep 20, 2025 · 6 min read
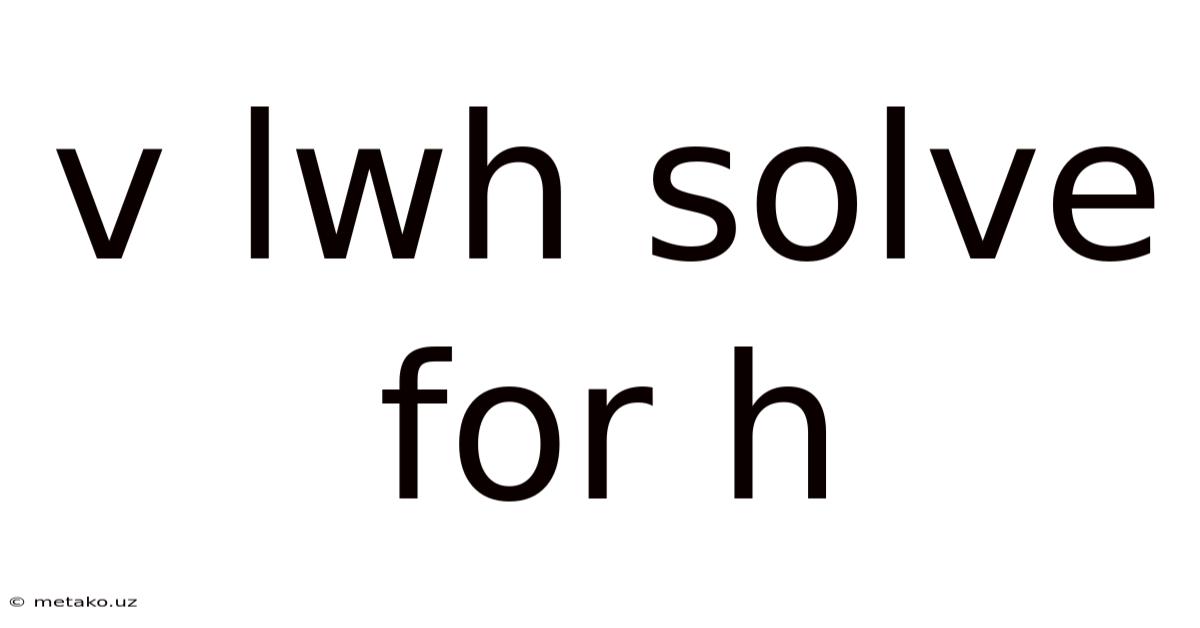
Table of Contents
Solving for h: A Deep Dive into the V = lwh Formula
Understanding the volume of a rectangular prism – often visualized as a box – is a fundamental concept in geometry and has widespread applications in various fields. The formula, V = lwh, represents this relationship, where 'V' stands for volume, 'l' for length, 'w' for width, and 'h' for height. This article will explore the formula V = lwh, focusing specifically on how to solve for 'h' (height), providing step-by-step instructions, explaining the underlying mathematical principles, and addressing frequently asked questions. We'll also examine real-world applications of this formula and delve into more complex scenarios.
Understanding the V = lwh Formula
Before we dive into solving for 'h', let's solidify our understanding of the formula itself. The formula V = lwh calculates the volume of a rectangular prism by multiplying its length (l), width (w), and height (h). Each of these dimensions represents a linear measurement (usually in centimeters, meters, inches, or feet). The resulting volume (V) is a cubic measurement (e.g., cubic centimeters, cubic meters).
Solving for h: A Step-by-Step Guide
To solve for 'h' in the equation V = lwh, we need to isolate 'h' on one side of the equation using algebraic manipulation. Here's a step-by-step guide:
-
Start with the original formula: V = lwh
-
Divide both sides by 'lw': To isolate 'h', we need to get rid of 'l' and 'w' that are multiplied with 'h'. We do this by dividing both sides of the equation by 'lw'. This gives us:
V/lw = (lwh)/lw
-
Simplify: The 'l' and 'w' on the right-hand side cancel out, leaving us with:
h = V/lw
Therefore, the formula to solve for height (h) is: h = V/lw
Example Problems: Putting it into Practice
Let's work through a few examples to reinforce our understanding.
Example 1:
A rectangular box has a volume of 120 cubic centimeters, a length of 10 centimeters, and a width of 4 centimeters. Find the height of the box.
- Known values: V = 120 cm³, l = 10 cm, w = 4 cm
- Formula: h = V/lw
- Solution: h = 120 cm³ / (10 cm * 4 cm) = 120 cm³ / 40 cm² = 3 cm
Therefore, the height of the box is 3 centimeters.
Example 2:
A storage container has a volume of 2.5 cubic meters, a length of 1.5 meters, and a height of 0.5 meters. Find the width of the container.
Notice that this example is subtly different: We are asked to find the width, not the height, but the principles remain the same.
- Known values: V = 2.5 m³, l = 1.5 m, h = 0.5 m
- Formula: We need to rearrange the basic formula to solve for width (w): w = V/(lh)
- Solution: w = 2.5 m³ / (1.5 m * 0.5 m) = 2.5 m³ / 0.75 m² = 3.33 meters (approximately)
Therefore, the width of the storage container is approximately 3.33 meters.
The Mathematical Principles Behind the Formula
The formula V = lwh is derived from the fundamental concept of volume calculation. Imagine building a rectangular prism using unit cubes (cubes with sides of length 1). To fill the base of the prism, you would need 'l' x 'w' unit cubes. Since the height is 'h', you would need to stack 'h' layers of these base unit cubes to form the complete prism. Hence, the total number of unit cubes, and thus the volume, is given by l x w x h.
Beyond the Basics: Real-World Applications
The ability to solve for the height (or any dimension) using V = lwh extends far beyond basic geometry problems. It has crucial applications in various fields:
- Engineering: Calculating the volume of materials needed for construction projects (e.g., concrete foundations, storage tanks). Determining the size of containers or components in mechanical design.
- Architecture: Estimating the volume of rooms, buildings, or spaces. This is crucial for HVAC (Heating, Ventilation, and Air Conditioning) system design and resource allocation.
- Logistics and Shipping: Calculating the capacity of shipping containers or determining the optimal dimensions for packaging to maximize space utilization and minimize shipping costs.
- Medicine: In certain medical procedures, the calculation of volumes is crucial for administering the correct dosages of medications.
- Agriculture: Calculating the volume of soil needed for planting, or the volume of water in irrigation systems.
These applications highlight the practical importance of mastering the formula V = lwh and the ability to solve for any of its variables.
Handling More Complex Scenarios
While the basic application is straightforward, some scenarios might introduce added complexity:
- Units Conversion: Ensure all measurements are in the same units before applying the formula. Converting between units (e.g., centimeters to meters) is often necessary for accurate calculations.
- Unknown Variables: Problems might provide only two dimensions and the volume, requiring you to solve for the missing dimension. The process remains the same; rearrange the formula accordingly.
- Composite Shapes: Some problems might involve shapes that are a combination of rectangular prisms. In such cases, you'll need to break down the composite shape into individual rectangular prisms, calculate the volume of each, and then add them together to find the total volume.
Frequently Asked Questions (FAQ)
Q1: What if I don't know the volume?
A1: If the volume (V) is unknown, you cannot solve for 'h' (or any other dimension) using the formula V = lwh. You would need additional information, such as the surface area of the prism or other relevant relationships.
Q2: Can this formula be used for other shapes?
A2: No, this formula is specifically for rectangular prisms (boxes). Other shapes, such as cylinders, spheres, or cones, require different volume formulas.
Q3: What happens if one of the dimensions is zero?
A3: If the length, width, or height is zero, the volume is automatically zero. A rectangular prism with a dimension of zero would not exist in three-dimensional space.
Q4: What if I have a problem with more than one unknown variable?
A4: You'll need more than one equation to solve the problem. Additional information, such as the surface area or other relationships between the variables, will be required. This often leads to the solution of simultaneous equations.
Conclusion
The ability to solve for 'h' (height) using the formula V = lwh is a valuable skill with numerous real-world applications. By understanding the formula's derivation and mastering the algebraic manipulation involved, you can confidently tackle various problems, from basic geometry exercises to complex engineering challenges. Remember to pay attention to units, handle unknown variables systematically, and break down complex problems into simpler components when necessary. This formula is a cornerstone of understanding spatial relationships and provides a solid foundation for further exploration in geometry and related fields. Mastering this simple equation will unlock a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
The Process Of Interpersonal Communication
Sep 21, 2025
-
What Will Lipids Dissolve In
Sep 21, 2025
-
First Vs Second Order Reactions
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about V Lwh Solve For H . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.