What's Bigger 5/8 Or 3/4
metako
Sep 14, 2025 · 5 min read
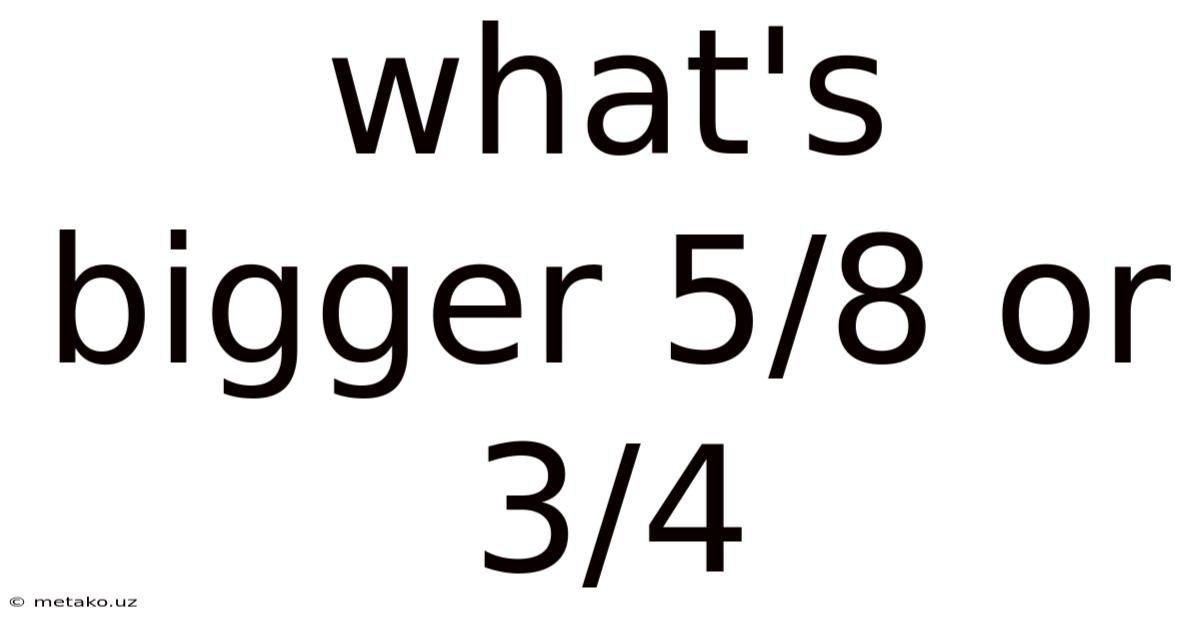
Table of Contents
Deciphering Fractions: Which is Bigger, 5/8 or 3/4? A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This comprehensive guide will not only definitively answer the question, "What's bigger, 5/8 or 3/4?", but will also equip you with the tools and knowledge to confidently compare any two fractions. We’ll explore various methods, delve into the underlying principles, and address common misconceptions, ensuring you grasp the concept fully. This guide is perfect for students, teachers, and anyone looking to refresh their understanding of fractions.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the denominator (4) tells us the whole is divided into four equal parts, and the numerator (3) indicates we're considering three of those parts.
To compare fractions, we need a common reference point. This is where finding a common denominator or converting fractions to decimals comes into play. Let's explore both methods in detail.
Method 1: Finding a Common Denominator
This is arguably the most fundamental method for comparing fractions. The principle is simple: to compare two fractions, we need to express them with the same denominator. This allows for a direct comparison of their numerators.
Steps:
-
Find the Least Common Multiple (LCM) of the denominators: The LCM is the smallest number that is a multiple of both denominators. For 5/8 and 3/4, the denominators are 8 and 4. The multiples of 4 are 4, 8, 12, 16... and the multiples of 8 are 8, 16, 24... The LCM of 4 and 8 is 8.
-
Convert the fractions to equivalent fractions with the LCM as the denominator: To convert 3/4 to an equivalent fraction with a denominator of 8, we need to multiply both the numerator and the denominator by the same number. Since 4 x 2 = 8, we multiply both the numerator and denominator of 3/4 by 2: (3 x 2) / (4 x 2) = 6/8.
-
Compare the numerators: Now we have 5/8 and 6/8. Since 6 > 5, we can conclude that 6/8 is greater than 5/8.
Therefore, 3/4 is bigger than 5/8.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them into decimals. This involves dividing the numerator by the denominator.
Steps:
-
Convert 5/8 to a decimal: Divide 5 by 8: 5 ÷ 8 = 0.625
-
Convert 3/4 to a decimal: Divide 3 by 4: 3 ÷ 4 = 0.75
-
Compare the decimals: Since 0.75 > 0.625, we conclude that 3/4 is greater than 5/8.
Visual Representation: Understanding the Size Difference
Visual aids can significantly enhance understanding. Imagine two identical pizzas.
-
3/4 Pizza: One pizza is cut into four equal slices, and you have three of them.
-
5/8 Pizza: The other pizza is cut into eight equal slices, and you have five of them.
Although you have more slices in the second pizza (five compared to three), each slice is smaller. The three larger slices from the first pizza represent a greater portion of the whole pizza than the five smaller slices from the second pizza. This visual representation clearly illustrates why 3/4 is larger than 5/8.
A Deeper Dive: Mathematical Principles Behind Fraction Comparison
The methods outlined above rely on fundamental mathematical principles:
-
Equivalence of Fractions: Multiplying or dividing both the numerator and denominator of a fraction by the same non-zero number results in an equivalent fraction. This principle is crucial for finding common denominators.
-
Properties of Inequalities: The comparison of fractions boils down to comparing their numerical values. The greater the numerical value, the larger the fraction.
-
Least Common Multiple (LCM): Finding the LCM ensures that we use the smallest possible denominator for comparison, making the calculation simpler and less prone to errors.
Frequently Asked Questions (FAQ)
Q1: Are there other methods to compare fractions?
A1: Yes, you can also use cross-multiplication. To compare a/b and c/d, you multiply a by d and b by c. If ad > bc, then a/b > c/d. However, the common denominator and decimal conversion methods are generally considered more intuitive and easier to understand, particularly for beginners.
Q2: What if the fractions have different signs (positive and negative)?
A2: Positive fractions are always greater than negative fractions. If you are comparing a positive and a negative fraction, the positive fraction will always be bigger.
Q3: How can I improve my skills in comparing fractions?
A3: Practice is key! Work through various examples, using both the common denominator and decimal conversion methods. Try visualizing the fractions as parts of a whole. Use online resources, worksheets, and interactive exercises to build your confidence and proficiency.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill with wide-ranging applications. This guide has provided a comprehensive understanding of how to compare fractions, emphasizing both the "how" and the "why". By mastering the methods of finding a common denominator and converting to decimals, coupled with a solid grasp of the underlying mathematical principles, you can confidently tackle any fraction comparison problem. Remember, consistent practice is crucial to developing fluency and accuracy in working with fractions. The ability to compare fractions effectively is not only essential for academic success but also a valuable life skill applicable in various real-world situations.
Latest Posts
Latest Posts
-
What Makes A Weak Base
Sep 14, 2025
-
Gas Liquid Solid Periodic Table
Sep 14, 2025
-
How To Find Line Integral
Sep 14, 2025
-
Coefficient Of A Chemical Equation
Sep 14, 2025
-
Power Functions And Polynomial Functions
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What's Bigger 5/8 Or 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.