X 2 X 2 6
metako
Sep 24, 2025 · 6 min read
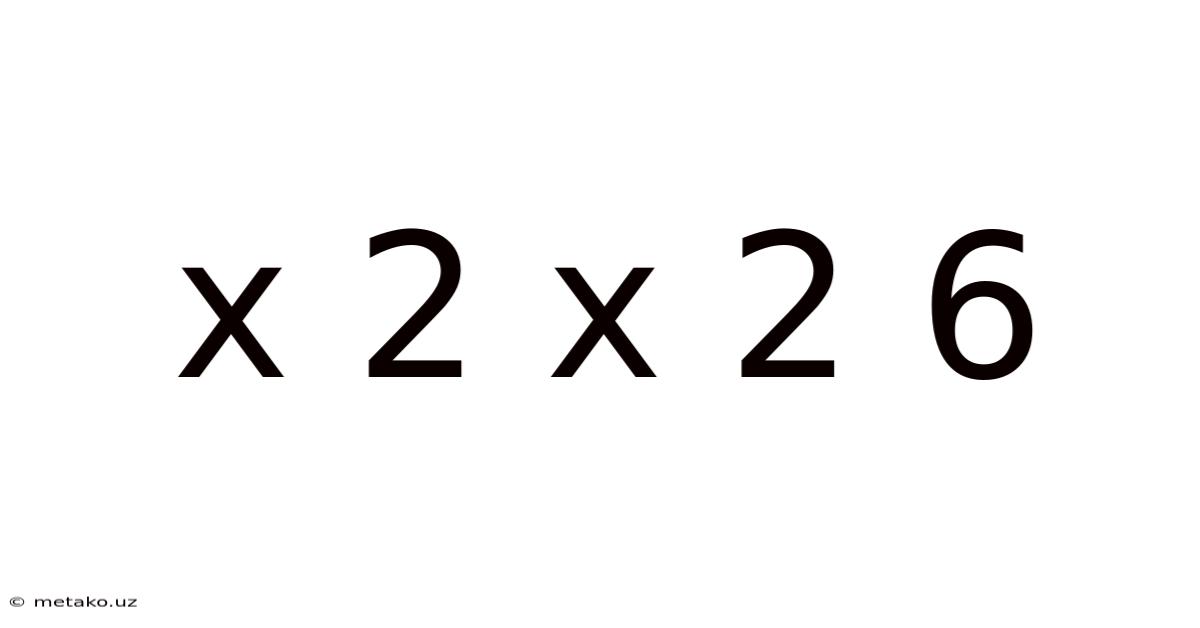
Table of Contents
Decoding the Enigma: Exploring the Mathematical and Logical Possibilities of "x 2 x 2 = 6"
This article delves into the intriguing mathematical puzzle presented by the equation "x 2 x 2 = 6." At first glance, this seems like a simple algebraic problem. However, a deeper exploration reveals a fascinating interplay of mathematical operations, logical reasoning, and the importance of defining our terms precisely. We'll unpack the various interpretations and solutions, highlighting the crucial role of context in determining the "correct" answer.
Introduction: Unveiling the Ambiguity
The equation "x 2 x 2 = 6" is inherently ambiguous. The lack of explicit operators between the variables and numbers leaves room for multiple interpretations. This ambiguity is precisely what makes this seemingly simple equation so rich in its potential for exploration and learning. We'll examine several approaches to solving this puzzle, demonstrating how subtle changes in interpretation can drastically alter the outcome. The journey will not only resolve potential solutions but also illuminate the importance of clear communication and precise mathematical notation.
Interpretation 1: Standard Algebraic Approach
The most straightforward interpretation assumes standard order of operations (PEMDAS/BODMAS). This means multiplication is performed from left to right. In this case, the equation becomes:
x * 2 * x * 2 = 6
This simplifies to:
4x² = 6
Solving for x, we get:
x² = 6/4 = 3/2
x = ±√(3/2) ≈ ±1.22
Therefore, under this interpretation, x has two possible solutions: approximately 1.22 and -1.22. This approach highlights the importance of understanding the order of operations and the potential for multiple solutions in algebraic equations.
Interpretation 2: Exploring Alternative Operations
Let's consider the possibility that the "2"s aren't strictly multipliers. Perhaps they represent a different operation altogether. For example:
- Exponentiation: If "2" signifies raising to the power of 2, the equation changes to:
x² * x² = 6
This simplifies to:
x⁴ = 6
x = ±⁶√6 ≈ ±1.565
This yields two different solutions, approximately 1.565 and -1.565. This showcases how a change in operational interpretation significantly alters the solution.
- Concatenation: In some programming contexts, juxtaposing numbers can imply concatenation (stringing them together). If we consider this, "x 2 x 2" could represent a string like "x2x2," and the equation makes no mathematical sense. This underlines the critical role of context and the importance of clearly defining the type of data being manipulated.
Interpretation 3: Introducing Parentheses and Functional Notation
Parentheses significantly impact the order of operations. Let's consider some possibilities:
-
(x2) x 2 = 6: This simplifies to 2x² = 6, yielding x² = 3, and x = ±√3 ≈ ±1.732.
-
x (2x2) = 6: This becomes 4x = 6, which solves to x = 3/2 = 1.5.
-
x(2 x 2) = 6: This simplifies to 4x = 6, which also gives x = 1.5.
These examples demonstrate the power of parentheses in controlling the order of operations and subsequently shaping the solution. This emphasizes the necessity of using parentheses for clarity, particularly when dealing with more complex equations. Mathematical notation needs to be unambiguous to avoid misinterpretations.
Interpretation 4: A Geometric Perspective
We can also approach this puzzle from a geometrical perspective. Could "x 2 x 2" represent dimensions? For instance, imagine a rectangular prism with dimensions x, 2, and 2. If the volume of this prism is 6, we have:
x * 2 * 2 = 6
This simplifies to 4x = 6, resulting in x = 1.5. This interpretation highlights the versatility of mathematical concepts and their application across different fields. It underscores that the same equation can represent different real-world scenarios.
Expanding the Scope: Beyond Simple Arithmetic
While the initial puzzle focused on basic arithmetic, we can expand its scope. Let's introduce functions:
- Let f(x) = x 2 x 2: This notation allows us to represent the expression more formally. We could then investigate the properties of this function, such as its domain, range, and behavior as x approaches infinity or negative infinity. We could also analyze its derivative and integral to further explore its characteristics. This transition into functional analysis shows how a simple equation can form the basis for much deeper mathematical exploration.
The Importance of Precise Mathematical Notation
This exploration underscores the critical role of precise mathematical notation. The ambiguity inherent in the original equation "x 2 x 2 = 6" arises directly from the lack of explicit operators. The placement of parentheses or the use of functional notation dramatically alters the meaning and the solution. This emphasizes the need for clarity and precision in mathematical writing to avoid confusion and ensure accurate communication of mathematical ideas. A simple omission can lead to significantly different results.
Logical Reasoning and Problem-Solving Strategies
Solving the "x 2 x 2 = 6" puzzle goes beyond simply calculating a numerical answer. It involves employing logical reasoning skills to consider multiple interpretations and systematically explore different approaches. It highlights the importance of:
- Considering all possibilities: The puzzle encourages a thorough exploration of potential meanings and operations.
- Systematic elimination: Once an interpretation is chosen, employing a methodical approach to solve the resulting equation is vital.
- Verification: After obtaining a solution, checking its validity within the chosen context is essential.
These problem-solving skills are transferable to various fields, reinforcing the importance of this seemingly simple mathematical exercise.
Frequently Asked Questions (FAQ)
Q: Is there one correct answer to "x 2 x 2 = 6"?
A: No, there isn't a single "correct" answer. The ambiguity in the equation allows for multiple interpretations, each leading to a different solution. The correctness of a solution depends entirely on the chosen interpretation and the context in which the equation is presented.
Q: How can I avoid ambiguity in my mathematical equations?
A: Always use explicit operators and parentheses to clarify the order of operations. Avoid relying on implicit assumptions. Clearly define the meaning of your variables and any unconventional notation you use.
Q: What mathematical concepts are relevant to solving this problem?
A: The problem involves order of operations (PEMDAS/BODMAS), algebraic manipulation, solving quadratic equations, understanding functional notation, and applying logical reasoning and problem-solving skills.
Q: What if the equation was "x * 2 * x * 2 = 6"? How would this change the solution?
A: This explicit use of the multiplication operator removes the ambiguity. Following the order of operations, we would solve 4x² = 6, leading to x = ±√(3/2) ≈ ±1.22.
Conclusion: The Power of Ambiguity in Mathematical Learning
The seemingly simple equation "x 2 x 2 = 6" proves to be a surprisingly rich and multifaceted puzzle. Its ambiguity highlights the crucial role of precise mathematical notation, the importance of considering various interpretations, and the necessity of applying logical reasoning and problem-solving skills. This seemingly simple exercise becomes a powerful tool for understanding the nuances of mathematical operations and the importance of clear communication in mathematics. It's a reminder that even seemingly straightforward problems can hold significant depth and lead to valuable insights into the world of mathematics and problem-solving. The journey of exploring this equation transcends the simple act of finding "x"; it’s about developing a deeper appreciation for the power and beauty of mathematics itself.
Latest Posts
Latest Posts
-
What Colour Does Magnesium Burn
Sep 24, 2025
-
Onion Root Tip Mitosis Stages
Sep 24, 2025
-
Snap Crackle And Pop Physics
Sep 24, 2025
-
Parent Graph Of Exponential Function
Sep 24, 2025
-
Homologous And Non Homologous Recombination
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 2 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.