X 2 X Sqrt X
metako
Sep 22, 2025 · 6 min read
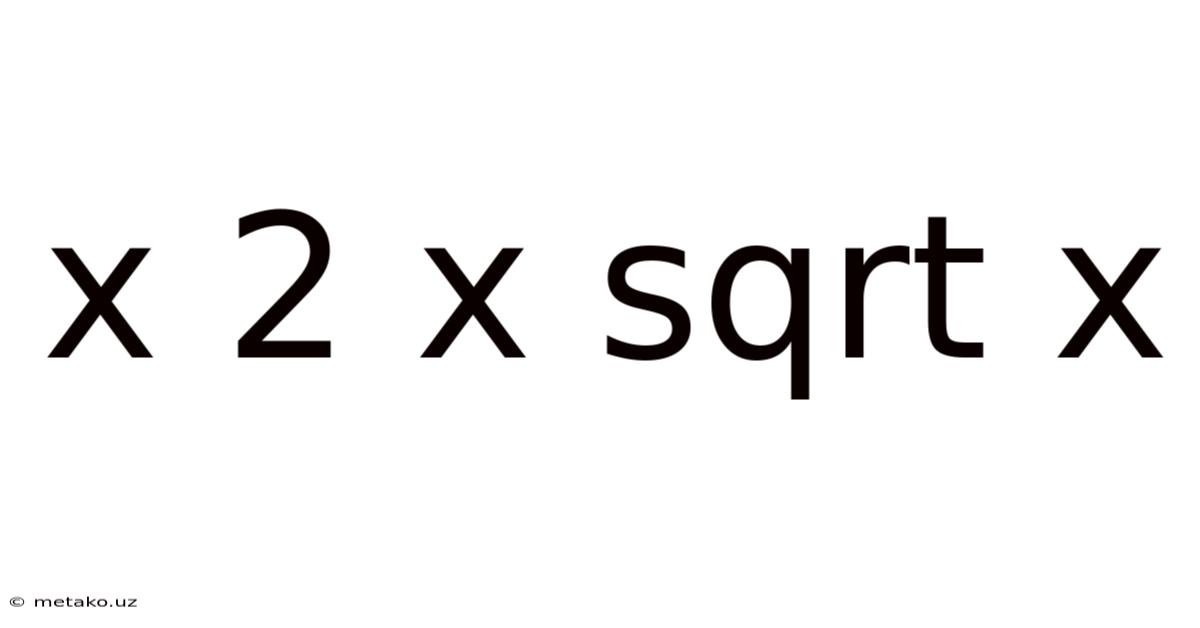
Table of Contents
Decoding x² * √x: A Comprehensive Exploration of Algebraic Expressions
Understanding algebraic expressions is fundamental to mastering mathematics. This article delves deep into the seemingly simple expression x² * √x, exploring its simplification, applications, and underlying mathematical principles. We'll cover its manipulation using exponent rules, its graphical representation, and address frequently asked questions, making this a comprehensive guide for students and enthusiasts alike. This exploration will equip you with a stronger understanding of algebraic manipulation and its practical implications.
Introduction: Understanding the Components
The expression x² * √x involves two key components:
-
x²: This represents 'x' multiplied by itself twice (x * x), or 'x' raised to the power of 2. This is a straightforward quadratic term.
-
√x: This represents the square root of 'x', also written as x<sup>1/2</sup>. This means finding a number which, when multiplied by itself, equals x.
The entire expression, x² * √x, signifies the product of these two terms. Our goal is to simplify this expression into a more concise and manageable form.
Simplifying x² * √x using Exponent Rules
The most efficient method to simplify x² * √x is through the application of exponent rules. Remember these crucial rules:
-
Product Rule: x<sup>a</sup> * x<sup>b</sup> = x<sup>a+b</sup> (When multiplying terms with the same base, add the exponents.)
-
Fractional Exponents: √x = x<sup>1/2</sup> (The square root of a number is equivalent to raising that number to the power of one-half.)
Applying these rules to our expression:
x² * √x = x² * x<sup>1/2</sup>
Using the product rule:
x² * x<sup>1/2</sup> = x<sup>(2 + 1/2)</sup> = x<sup>(5/2)</sup>
Therefore, the simplified form of x² * √x is x<sup>5/2</sup>. This is a significantly more concise representation of the original expression.
Graphical Representation and Analysis
Visualizing the expression helps in understanding its behavior. Let's consider the graph of y = x<sup>5/2</sup>.
-
Domain: The domain of the function is x ≥ 0, because we cannot take the square root of a negative number within the real number system.
-
Range: The range of the function is y ≥ 0. The function will always output non-negative values.
-
Behavior: The graph is an increasing function for x ≥ 0. As x increases, y increases at an increasing rate. This indicates a non-linear relationship between x and y.
The graph would exhibit a steeper incline as x gets larger, showcasing the rapid growth characteristic of functions with exponents greater than 1. This visualization solidifies our understanding of the expression's behavior across different values of x.
Practical Applications of x<sup>5/2</sup>
While seemingly abstract, the expression x<sup>5/2</sup>, and its equivalent x²√x, has applications in various fields:
-
Physics: Certain physical phenomena, such as the relationship between energy and frequency in quantum mechanics, or the diffusion of particles, might involve expressions similar to x<sup>5/2</sup>. The exponent might reflect the dimensionality of the system or the nature of the process involved.
-
Engineering: In engineering design, such expressions might emerge during calculations involving scaling, areas, or volumes, particularly when dealing with relationships where the square root is a factor, such as in calculations involving fluid dynamics or stress on materials.
-
Economics and Finance: In models related to growth or scaling, such an expression might represent a non-linear growth trajectory. For example, the impact of increased investment might grow non-linearly with respect to initial capital, potentially fitting a model incorporating a square root component.
-
Computer Science: Algorithm analysis sometimes involves expressions with fractional exponents, often reflecting the complexity of a specific operation within the algorithm. The value of x could represent input size, with the expression describing the time or space complexity.
These examples, while not exhaustive, demonstrate the potential relevance of this seemingly basic expression in various fields. The specific context determines the meaning and interpretation of x and the resulting value.
Further Exploration: Extending the Concept
We can extend our understanding by considering variations on this expression:
-
x<sup>n</sup> * √x: This generalizes our initial problem. Using the same exponent rules, we can simplify this to x<sup>(n + 1/2)</sup>.
-
Other Roots: Instead of the square root, we could consider cube roots (x<sup>1/3</sup>), fourth roots (x<sup>1/4</sup>), and so on. The principles of exponent manipulation remain the same. For instance, x² * ³√x would simplify to x<sup>(2 + 1/3)</sup> = x<sup>7/3</sup>.
-
Negative Exponents: Exploring the expression with negative exponents adds further complexity. The expression x<sup>-5/2</sup> would be equivalent to 1 / x<sup>5/2</sup>, introducing the concept of reciprocals and further emphasizing the versatility of exponent rules.
These extensions highlight the power and flexibility of the fundamental exponent rules in simplifying and manipulating complex algebraic expressions.
Frequently Asked Questions (FAQ)
-
Q: Can I always simplify expressions involving roots and powers in this manner?
- A: Yes, as long as the terms involve the same base variable (in this case, x). The exponent rules provide a systematic way to simplify such expressions.
-
Q: What if I have different variables within the expression?
- A: If the expression involves different variables, simplification becomes more limited. You might be able to factor out common terms, but a direct simplification using exponent rules, as demonstrated above, is not possible.
-
Q: What if x is negative?
- A: In the real number system, the square root of a negative number is not defined. Therefore, the expression x² * √x is only defined for non-negative values of x (x ≥ 0). If you are working in the complex number system, the situation changes, but that's a topic for a more advanced discussion.
-
Q: Are there other ways to simplify x² * √x?
- A: While the method using exponent rules is the most efficient and mathematically rigorous, you could potentially expand the expression to (x * x) * √x and then manipulate it, but this approach is less concise and more prone to errors than utilizing the exponent rules.
Conclusion: Mastering Algebraic Manipulation
This article provided a thorough exploration of the algebraic expression x² * √x, demonstrating its simplification using exponent rules, analyzing its graphical representation, highlighting its potential applications, and addressing common questions. Understanding this seemingly simple expression provides a solid foundation for tackling more complex algebraic manipulations. The mastery of exponent rules is crucial not only for simplifying expressions but also for solving equations, understanding functions, and applying mathematical concepts across various disciplines. By focusing on fundamental principles and applying logical steps, you can confidently approach and solve a wider range of mathematical problems. Remember that continued practice and exploration are key to mastering these concepts.
Latest Posts
Latest Posts
-
Diagram Of A Frogs Mouth
Sep 22, 2025
-
Is Nacl Ionic Or Molecular
Sep 22, 2025
-
Biology By Peter Raven Pdf
Sep 22, 2025
-
Carbon Monoxide Ionic Or Covalent
Sep 22, 2025
-
Chimpanzee Skeleton Vs Human Skeleton
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 2 X Sqrt X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.