X 2 Y 2 Z
metako
Sep 16, 2025 · 6 min read
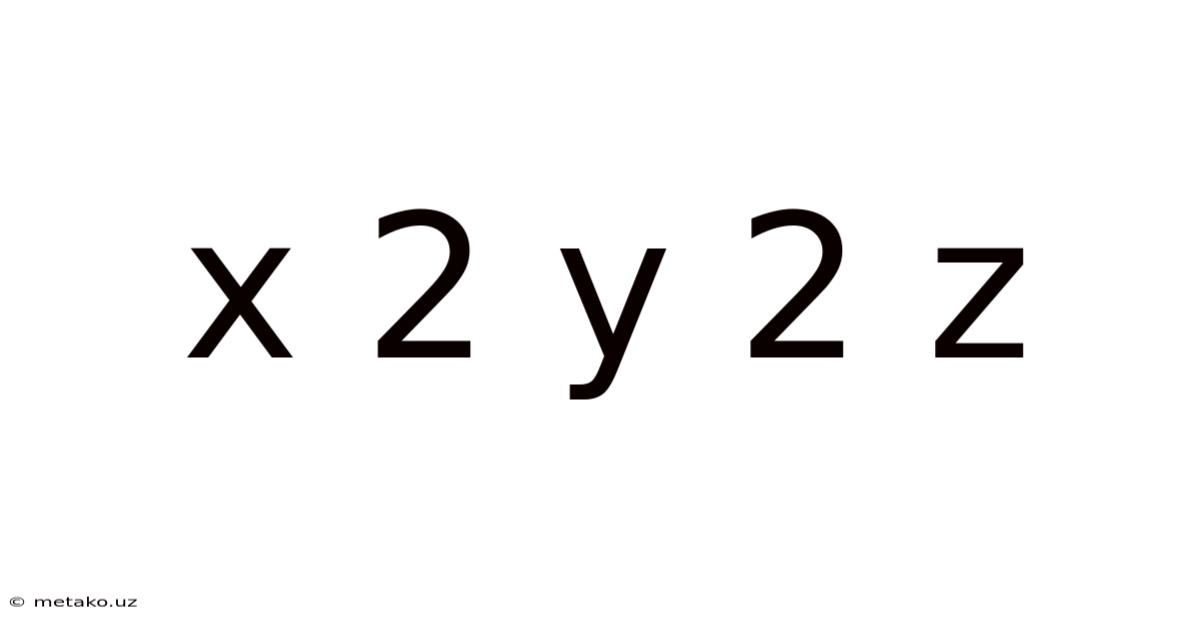
Table of Contents
Unveiling the Mysteries of x² + y² + z²: A Deep Dive into Sums of Squares
The expression x² + y² + z² represents the sum of the squares of three variables, x, y, and z. This seemingly simple algebraic expression holds significant importance across various branches of mathematics, from basic algebra and geometry to advanced topics like number theory and linear algebra. This comprehensive article will explore this expression in detail, examining its properties, applications, and implications. We'll delve into its geometric interpretation, its role in proving theorems, and explore some of the fascinating mathematical puzzles it presents. Understanding x² + y² + z² is key to unlocking a deeper appreciation for the elegance and power of mathematical concepts.
Understanding the Fundamentals: A Simple Introduction
Before we dive into the intricacies, let's establish a foundational understanding. The expression x² + y² + z² simply means adding together the squares of three individual numbers. For example, if x = 2, y = 3, and z = 4, then x² + y² + z² = 2² + 3² + 4² = 4 + 9 + 16 = 29. This is straightforward calculation, but the implications of this seemingly simple operation extend far beyond this basic arithmetic.
The Geometric Interpretation: Visualizing the Equation
One of the most illuminating ways to understand x² + y² + z² is through its geometric interpretation. In three-dimensional space, this expression represents the squared distance from the origin (0, 0, 0) to a point with coordinates (x, y, z). This is a direct consequence of the Pythagorean theorem extended to three dimensions. Imagine a right-angled triangle with legs of length x and y lying in the xy-plane. The hypotenuse of this triangle, using the Pythagorean theorem, has length √(x² + y²). Now, consider this hypotenuse as the base of another right-angled triangle, with the height being z, which is perpendicular to the xy-plane. The hypotenuse of this second triangle, connecting the origin to the point (x, y, z), has length √(x² + y² + z²). Thus, x² + y² + z² gives us the square of this distance.
This geometric representation provides valuable insight. For instance, the equation x² + y² + z² = r² represents a sphere centered at the origin with radius r. Every point (x, y, z) satisfying this equation lies on the surface of this sphere. This simple equation encapsulates a fundamental geometric concept.
Applications in Various Fields: Beyond the Basics
The expression x² + y² + z² finds applications in numerous mathematical and scientific fields:
-
Physics: In physics, especially in mechanics and electromagnetism, this expression frequently appears when calculating distances, energies, and forces in three-dimensional space. For example, in classical mechanics, the kinetic energy of a particle with mass m and velocity components vx, vy, and vz is given by (1/2)m(vx² + vy² + vz²). The magnitude of a vector with components x, y, and z is √(x² + y² + z²), a crucial concept in vector analysis.
-
Computer Graphics: In computer graphics, the equation x² + y² + z² is fundamental for rendering three-dimensional objects and scenes. It's used in calculating distances between points, determining visibility, and applying lighting effects.
-
Number Theory: In number theory, the sum of squares plays a crucial role in problems involving integer solutions to equations. For example, Fermat's theorem on sums of two squares deals with when an integer can be expressed as the sum of two squares, and this concept extends to three squares and beyond. Investigating the conditions under which an integer can be represented as the sum of three squares is a complex and fascinating area of research. Lagrange's four-square theorem states that every natural number can be represented as the sum of at most four integer squares.
-
Linear Algebra: In linear algebra, the expression x² + y² + z² is related to the concept of the norm (or magnitude) of a vector in three-dimensional Euclidean space. The norm is a fundamental concept for understanding vector spaces and their properties.
Advanced Concepts and Extensions: Delving Deeper
The expression x² + y² + z² provides a stepping stone to more advanced mathematical concepts. Let's explore some of them:
-
Sums of More Than Three Squares: The concept extends naturally to higher dimensions. In n-dimensional space, the squared distance from the origin to a point (x₁, x₂, ..., xₙ) is given by x₁² + x₂² + ... + xₙ². This has profound implications in higher-dimensional geometry and algebra.
-
Ellipsoids and Other Quadric Surfaces: More complex equations involving x² + y² + z², such as (x²/a²) + (y²/b²) + (z²/c²) = 1, represent ellipsoids, a three-dimensional generalization of an ellipse. Studying these equations leads to a deeper understanding of quadric surfaces.
-
Quaternion Algebra: Quaternions, an extension of complex numbers, involve four components, and the norm of a quaternion is related to the sum of the squares of its four components. Quaternions find applications in computer graphics, robotics, and other fields requiring efficient rotations in three-dimensional space.
-
Multivariate Calculus: In multivariate calculus, the expression frequently appears in partial derivatives and gradient calculations, particularly when dealing with functions of three variables.
Solving Problems Involving x² + y² + z²: Practical Applications
Let's look at a few examples illustrating how to work with this expression:
Example 1: Find the distance between the points (1, 2, 3) and (4, 5, 6).
To solve this, we first find the differences between the corresponding coordinates: (4-1) = 3, (5-2) = 3, (6-3) = 3. Then, we compute the sum of the squares of these differences: 3² + 3² + 3² = 27. The distance is the square root of this sum: √27 = 3√3.
Example 2: Find all points (x, y, z) such that x² + y² + z² = 9.
This equation represents a sphere centered at the origin with a radius of 3. Thus, any point (x, y, z) that satisfies x² + y² + z² = 9 lies on the surface of this sphere. There are infinitely many such points.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between x² + y² and x² + y² + z²?
- A: x² + y² represents the squared distance from the origin in two dimensions (a plane), while x² + y² + z² represents the squared distance from the origin in three dimensions (space).
-
Q: Can x, y, and z be negative numbers?
- A: Yes, x, y, and z can be any real numbers, including negative numbers. Squaring a negative number results in a positive number, so the sum of squares will always be non-negative.
-
Q: What are some real-world applications of this concept beyond mathematics and physics?
- A: Many areas utilize this principle indirectly. For instance, GPS systems rely on distance calculations in three-dimensional space, which fundamentally uses the Pythagorean theorem's extension reflected in x² + y² + z².
Conclusion: A Versatile Mathematical Expression
The expression x² + y² + z² serves as a fundamental building block across numerous mathematical disciplines and scientific applications. From its simple geometric interpretation as the squared distance in three-dimensional space to its complex roles in advanced concepts like number theory and linear algebra, this seemingly simple algebraic expression unveils profound insights into the structure and relationships within mathematical systems. Understanding this expression not only enriches one's mathematical knowledge but also provides a foundation for exploring more advanced mathematical concepts and applications in various fields. Its versatility and enduring importance make it a cornerstone of mathematical understanding. This exploration only scratches the surface of the richness and complexity associated with this fundamental mathematical construct. Further exploration into its properties and applications is encouraged for those seeking a deeper understanding of mathematics and its applications in the world around us.
Latest Posts
Latest Posts
-
Ph Of Milk Of Magnesia
Sep 16, 2025
-
United States History To 1877
Sep 16, 2025
-
Is Table Salt A Mixture
Sep 16, 2025
-
Plasma Membrane Is Composed Of
Sep 16, 2025
-
Related Rates Of A Sphere
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.