Lcm For 4 And 10
metako
Sep 12, 2025 · 6 min read
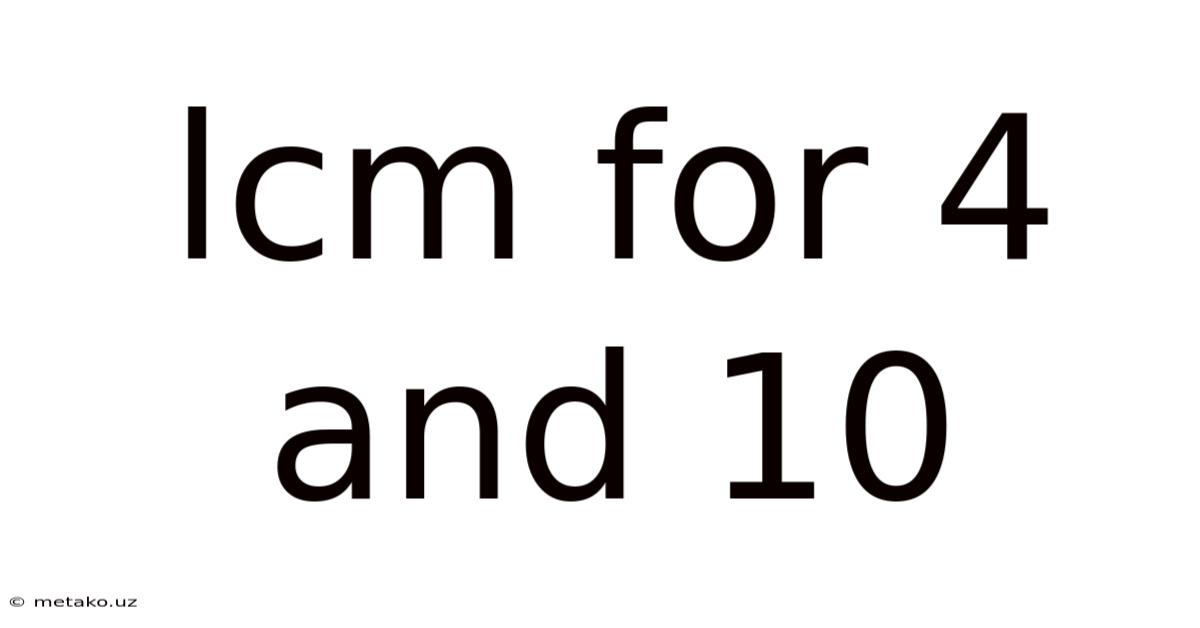
Table of Contents
Finding the LCM: A Deep Dive into the Least Common Multiple of 4 and 10
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to more advanced mathematical concepts. This article will not only show you how to find the LCM of 4 and 10 but will also delve into the why behind the methods, exploring different approaches and their applications. We'll cover various methods, including prime factorization, listing multiples, and using the greatest common divisor (GCD), ensuring a comprehensive understanding for learners of all levels. This exploration will equip you with the tools to tackle LCM problems for any pair of numbers, building a solid foundation in number theory.
Understanding Least Common Multiples (LCM)
Before we dive into finding the LCM of 4 and 10, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both numbers divide into evenly. Understanding this definition is crucial for grasping the various methods used to calculate the LCM.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 4 and 10. Let's list the multiples of each number:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 10: 10, 20, 30, 40, 50...
By comparing the lists, we can see that the smallest number that appears in both lists is 20. Therefore, the LCM of 4 and 10 is 20. This method works well for small numbers but becomes less efficient as the numbers increase in size.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Remember, a prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
-
Find the prime factorization of 4: 4 = 2 x 2 = 2²
-
Find the prime factorization of 10: 10 = 2 x 5
-
Identify the highest power of each prime factor: The prime factors are 2 and 5. The highest power of 2 is 2² (from the factorization of 4), and the highest power of 5 is 5¹ (from the factorization of 10).
-
Multiply the highest powers together: LCM(4, 10) = 2² x 5 = 4 x 5 = 20
Therefore, the LCM of 4 and 10 using prime factorization is 20. This method is more systematic and efficient, especially when dealing with larger numbers or multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The GCD, or greatest common divisor, is the largest number that divides both numbers without leaving a remainder. There's a handy relationship between the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
-
Find the GCD of 4 and 10: The common divisors of 4 and 10 are 1 and 2. The greatest common divisor is 2.
-
Apply the formula: LCM(4, 10) x GCD(4, 10) = 4 x 10
-
Solve for LCM: LCM(4, 10) x 2 = 40 => LCM(4, 10) = 40 / 2 = 20
This method elegantly connects the LCM and GCD, offering another efficient way to calculate the LCM, particularly beneficial when dealing with larger numbers where finding the GCD might be easier than directly finding the LCM. Various algorithms exist for efficiently calculating the GCD, such as the Euclidean algorithm.
The Importance of LCM in Real-World Applications
While finding the LCM might seem like an abstract mathematical exercise, it has practical applications in various fields:
-
Scheduling: Imagine two buses that leave a station at different intervals. Finding the LCM of their departure times helps determine when they will depart at the same time again.
-
Fractions: When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator, simplifying calculations.
-
Project Management: In project management, tasks might have different completion cycles. Understanding the LCM can help determine when all tasks can be completed simultaneously.
-
Music Theory: The LCM plays a role in music theory when determining the least common multiple of note durations. This helps in harmonizing different rhythms.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method we discussed earlier is not just a convenient technique; it reveals fundamental properties of numbers. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This theorem underpins much of number theory, providing a building block for understanding more complex mathematical structures. The uniqueness of the prime factorization allows us to systematically analyze the divisibility properties of numbers, crucial for many mathematical problems.
Addressing Common Questions (FAQ)
Q: What if the numbers share no common factors other than 1?
A: If the numbers are coprime (meaning their GCD is 1), the LCM is simply the product of the two numbers. For example, the LCM of 9 and 10 is 90 (because GCD(9,10) = 1).
Q: Can this method be extended to more than two numbers?
A: Yes, all the methods discussed—listing multiples, prime factorization, and using the GCD—can be extended to find the LCM of three or more numbers. For prime factorization, you'd consider the highest power of each prime factor present in any of the numbers. For the GCD method, you would iteratively calculate the GCD of pairs and then use the relationship to find the LCM.
Q: Why is the prime factorization method considered more efficient for larger numbers?
A: The prime factorization method provides a systematic approach, avoiding the potentially lengthy process of listing multiples for larger numbers. It directly uses the fundamental building blocks (prime factors) to construct the LCM, making it computationally more efficient.
Q: What are some alternative methods for finding the GCD?
A: The Euclidean algorithm is a highly efficient method for finding the greatest common divisor of two numbers. It uses repeated division to reduce the problem until the GCD is found.
Conclusion: Mastering the LCM
Finding the least common multiple, though seemingly simple, offers a gateway to a deeper understanding of number theory. This article has explored multiple approaches, highlighting the versatility and elegance of the prime factorization method, while also showcasing the connection between the LCM and GCD. By understanding these concepts and their applications, you're not just learning a mathematical technique; you're developing a fundamental skill applicable in diverse fields, from scheduling to music theory. Mastering the LCM is more than just finding a number; it's about understanding the fundamental structure of numbers themselves. Keep practicing, and you'll find yourself confidently tackling LCM problems of any complexity.
Latest Posts
Latest Posts
-
Common Stock Issuance Journal Entry
Sep 12, 2025
-
Addition Of Water To Alkene
Sep 12, 2025
-
Capacitor Charging And Discharging Equation
Sep 12, 2025
-
Lithium Molar Mass G Mol
Sep 12, 2025
-
Range Of Hearing Of Animals
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 4 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.