Lcm Of 14 And 35
metako
Sep 24, 2025 · 5 min read
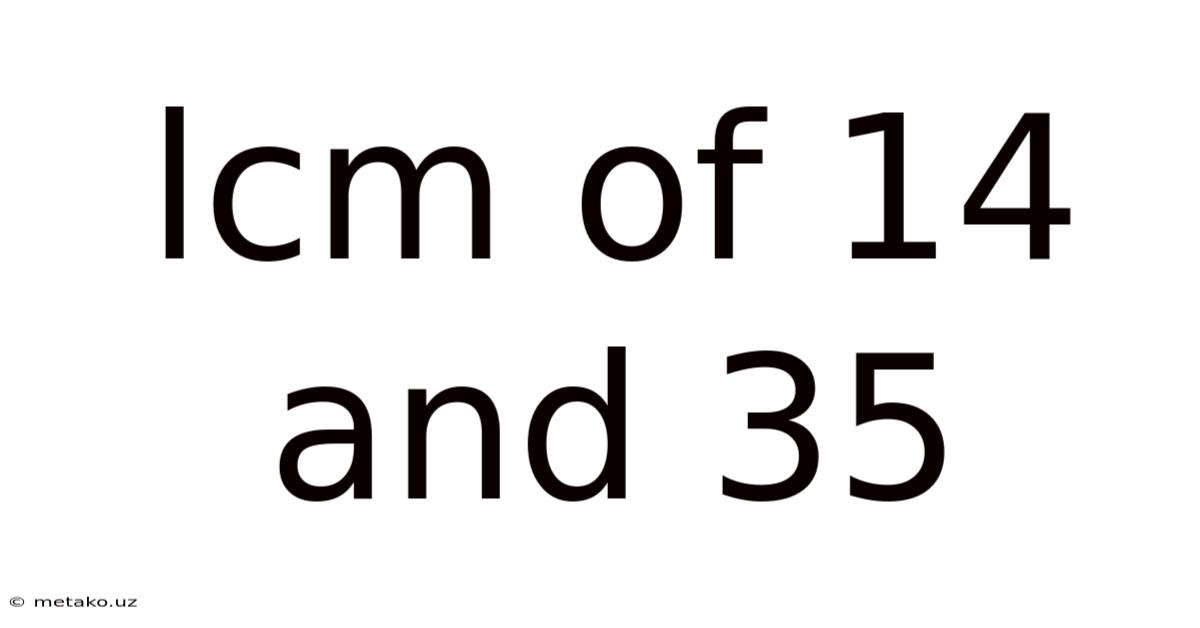
Table of Contents
Finding the LCM of 14 and 35: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to more advanced mathematical applications. This comprehensive guide will not only show you how to calculate the LCM of 14 and 35 but also explore the different methods, their underlying principles, and the broader significance of LCMs in various mathematical contexts. This article is designed for students learning about LCMs, as well as anyone looking to refresh their understanding of this fundamental concept.
Understanding Least Common Multiples (LCM)
Before diving into the specifics of finding the LCM of 14 and 35, let's establish a solid foundation. The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder.
For example, the multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... and the multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. Let's apply it to find the LCM of 14 and 35.
-
List the multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140...
-
List the multiples of 35: 35, 70, 105, 140, 175...
-
Identify the common multiples: Notice that 70 and 140 appear in both lists.
-
Determine the least common multiple: The smallest common multiple is 70. Therefore, the LCM of 14 and 35 is 70.
This method works well for smaller numbers, but it becomes less efficient as the numbers get larger. Imagine trying to find the LCM of 147 and 231 using this method! It would be quite tedious.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
-
Find the prime factorization of each number:
- 14: 2 x 7
- 35: 5 x 7
-
Identify common and uncommon prime factors: Both 14 and 35 share the prime factor 7. The uncommon prime factors are 2 and 5.
-
Construct the LCM: To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together. In this case:
LCM(14, 35) = 2 x 5 x 7 = 70
Therefore, the LCM of 14 and 35 is 70. This method is significantly more efficient than listing multiples, particularly when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are intimately related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
-
Find the GCD of 14 and 35: We can use the Euclidean algorithm for this.
- 35 = 2 x 14 + 7
- 14 = 2 x 7 + 0
The last non-zero remainder is the GCD, which is 7.
-
Apply the formula:
LCM(14, 35) x GCD(14, 35) = 14 x 35 LCM(14, 35) x 7 = 490 LCM(14, 35) = 490 / 7 = 70
Therefore, the LCM of 14 and 35 is 70. This method is also efficient and demonstrates the elegant relationship between LCM and GCD.
Why is LCM Important?
Understanding LCMs is crucial in many areas of mathematics and real-world applications. Here are some examples:
-
Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions. It allows you to find a common denominator, simplifying the calculation.
-
Scheduling: LCM is used to determine when events with different periodicities will occur simultaneously. For instance, if two buses arrive at a stop every 14 minutes and 35 minutes respectively, the LCM (70 minutes) tells you when they will arrive together.
-
Pattern Recognition: LCMs help identify repeating patterns in sequences. Understanding cycles and repetitions is crucial in various fields like cryptography and signal processing.
-
Measurement: In scenarios involving different measurement units, the LCM can help determine the smallest common unit for accurate comparison or conversion.
-
Abstract Algebra: The concept of LCM extends to more advanced mathematical structures like rings and fields.
Frequently Asked Questions (FAQ)
-
What if the numbers have no common factors? If two numbers are relatively prime (i.e., their GCD is 1), their LCM is simply their product. For example, LCM(5, 6) = 5 x 6 = 30 because 5 and 6 share no common factors other than 1.
-
Can I find the LCM of more than two numbers? Yes, you can extend the prime factorization method to find the LCM of multiple numbers. You would find the prime factorization of each number, identify all prime factors present, and then take the highest power of each prime factor to construct the LCM.
-
Is there a formula to directly calculate the LCM? While there's no single direct formula like for addition or multiplication, the formula connecting LCM and GCD provides an indirect way to calculate the LCM.
-
How do I choose the best method? For smaller numbers, listing multiples is a simple approach. For larger numbers, prime factorization is generally more efficient. Using the GCD method is also efficient and highlights the relationship between LCM and GCD.
Conclusion
Finding the LCM of 14 and 35, as demonstrated through three different methods, highlights the versatility and importance of this fundamental mathematical concept. The seemingly simple task of calculating the LCM reveals a deeper understanding of prime factorization, the relationship between LCM and GCD, and the broader applications of this concept in various fields of mathematics and beyond. Mastering LCM calculations not only strengthens your arithmetic skills but also provides a foundational understanding that will prove valuable in more advanced mathematical studies and real-world problem-solving. Remember to choose the method that best suits the numbers you are working with, always focusing on efficiency and accuracy.
Latest Posts
Latest Posts
-
What Are Life History Traits
Sep 24, 2025
-
Examples Of A Dot Plot
Sep 24, 2025
-
Definition Of Fracture In Minerals
Sep 24, 2025
-
X 2 X 2 6
Sep 24, 2025
-
Density Of Aluminum G Ml
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 14 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.